题目内容
函数y=x5-x3-2x,则下列判断正确的是( )A.在区间(-1,1)内函数为增函数
B.在区间(-∞,-1)内函数为减函数
C.在区间(-∞,1)内函数为减函数
D.在区间(1,+∞)内函数为增函数
分析:本题考查利用导数求函数单调区间的方法以及一元高次不等式的解法.
解:y′=5x4-3x2-2=(5x2+2)(x2-1)
=(5x2+2)(x+1)(x-1).
∵5x2+2>0恒成立,
∴当x∈(-1,1)时,y′<0,则f(x)为减函数;
当x∈(-∞,-1)或x∈(1,+∞)时,y′>0,则f(x)为增函数.故选D.
答案:D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
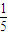 x5-
x5- x3+3x2+
x3+3x2+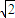 ;
; .
.