题目内容
.函数y=x5-x3-2x,则下列判断正确的是
- A.在区间(-1，1)内函数为增函数
- B.在区间(-∞，-1)内函数为减函数
- C.在区间(-∞，1)内函数为减函数
- D.在区间(1，+∞)内函数为增函数
D
本题考查利用导数求函数的单调区间，以及一元高次不等式的解法.
y′=5x4－3x2－2=(5x2＋2)(x2－1)=(5x2＋2)(x＋1)(x－1).
当x∈(－1,1)时，y′＜0,则f(x)为减函数；当x∈(－∞,－1)或x∈(1,＋∞)时，y′＞0，则f(x)为增函数.
本题考查利用导数求函数的单调区间，以及一元高次不等式的解法.
y′=5x4－3x2－2=(5x2＋2)(x2－1)=(5x2＋2)(x＋1)(x－1).
当x∈(－1,1)时，y′＜0,则f(x)为减函数；当x∈(－∞,－1)或x∈(1,＋∞)时，y′＞0，则f(x)为增函数.
练习册系列答案
相关题目
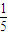,则f′(0)=0 ③加速度是动点位移函数s(t)对时间t的导数 ④函数y=x5的导函数的值恒非负
x5-
x3+3x2+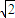
；
．