题目内容
求下列函数的导数:(1)y=
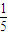 x5-
x5- x3+3x2+
x3+3x2+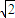 ;
;(2)y=(3x3-4x)(2x+1);
(3)y=
 .
.
【答案】分析:(1)根据求导公式(xn)'=nxn-1可得答案.
(2)将乘积展开,再由求导公式(xn)'=nxn-1可得答案.
(3)根据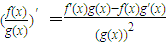 可得到答案.
可得到答案.
解答:解:(1)y′=( x5)′-(
x5)′-( x3)′+(3x2)′+(
x3)′+(3x2)′+(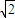 )′
)′
=x4-4x2+6x.
(2)法一:∵y=(3x3-4x)(2x+1)=6x4+3x3-8x2-4x,
∴y′=24x3+9x2-16x-4.
法二:y′=(3x3-4x)′(2x+1)+(3x3-4x)(2x+1)′
=(9x2-4)(2x+1)+(3x3-4x)•2
=24x3+9x2-16x-4.
(3)y′=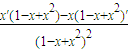
=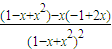 =
=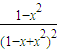 .
.
点评:本题主要考查求导公式的记忆和运算.属基础题.
(2)将乘积展开,再由求导公式(xn)'=nxn-1可得答案.
(3)根据
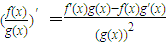 可得到答案.
可得到答案.解答:解:(1)y′=(
 x5)′-(
x5)′-( x3)′+(3x2)′+(
x3)′+(3x2)′+(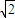 )′
)′=x4-4x2+6x.
(2)法一:∵y=(3x3-4x)(2x+1)=6x4+3x3-8x2-4x,
∴y′=24x3+9x2-16x-4.
法二:y′=(3x3-4x)′(2x+1)+(3x3-4x)(2x+1)′
=(9x2-4)(2x+1)+(3x3-4x)•2
=24x3+9x2-16x-4.
(3)y′=
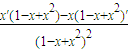
=
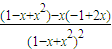 =
=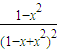 .
.点评:本题主要考查求导公式的记忆和运算.属基础题.

练习册系列答案
相关题目