题目内容
现有甲、乙、丙三人参加某电视台的应聘节目《非你莫属》,若甲应聘成功的概率为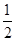 ,乙、丙应聘成功的概率均为
,乙、丙应聘成功的概率均为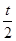 ,(0<t<2),且三个人是否应聘成功是相互独立的.
,(0<t<2),且三个人是否应聘成功是相互独立的.
(1)若乙、丙有且只有一个人应聘成功的概率等于甲应聘成功的概率,求t的值;
(2)记应聘成功的人数为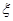 ,若当且仅当为
,若当且仅当为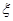 =2时概率最大,求E(
=2时概率最大,求E(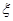 )的取值范围.
)的取值范围.
(1)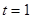 ;(2)
;(2)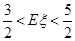
解析试题分析:(1)乙、丙有且只有一个人应聘成功分为乙成功且丙不成功和乙不成功且丙成功两种情况,根据相互独立事件有一个发生的概率公式列出关于t的方程,解之即可.
(2)写出随机变量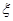 的所有可能取值,然后计算出相应的概率,列出分布列,求出E(
的所有可能取值,然后计算出相应的概率,列出分布列,求出E(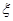 )的表达式,由于
)的表达式,由于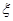 =2时概率最大,可得
=2时概率最大,可得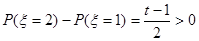 ,
,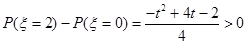 ,
, ,而0<t<2,解得
,而0<t<2,解得 ,即得E(
,即得E(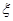 )的取值范围..
)的取值范围..
试题解析:(1)由题意得 ,解得
,解得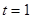 . 3分
. 3分
(2)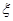 的所有可能取值为0,1,2,3
的所有可能取值为0,1,2,3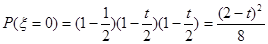 ;
;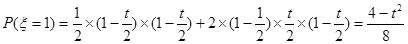 ;
;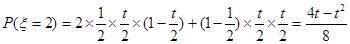 ;
;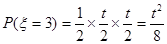 .
.
故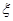 的分布列为:
的分布列为:
7分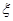
0 1 2 3 
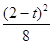
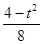
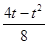
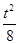
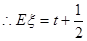 . 8分
. 8分
由题意得: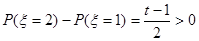 ,
,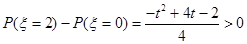 ,
, ,又因为
,又因为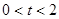
所以解得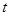 的取值范围是
的取值范围是 . 11分
. 11分 . 12分
. 12分
考点:1.相互独立事件的概率;2.随机变量的分布列和数学期望.

练习册系列答案
相关题目
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
| 重量段 | [80,85) | [85,90) | [90,95) | [95,100] |
| 件数 | 5 | a | 15 | b |
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.
 ,
,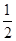 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为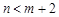 的概率.
的概率.