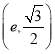题目内容
【题目】已知函数![]() 且
且![]()
(1)求该函数的值域;
(2)若![]() 对于任意
对于任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)令t=log2x,则可将函数在x∈[2,4]时的值域问题转化为二次函数在定区间上的值域问题,利用二次函数的图象分析出函数的最值,即可得到函数的值域;
(2)令t=log2x,则可将已知问题转化为![]() 对t∈[1,2]恒成立,求出不等号左边式子的最小值即可得到答案.
对t∈[1,2]恒成立,求出不等号左边式子的最小值即可得到答案.
(1) ![]() ,2≤x≤4,
,2≤x≤4,
设log2x=t,1≤t≤2,
∴f(t)=(t2)(![]() t
t![]() )=
)=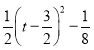
当![]() 时,
时, ![]() ,当t=1,或t=2时,ymax=0.
,当t=1,或t=2时,ymax=0.
∴函数的值域是![]() .
.
(2)若![]() 对于任意
对于任意![]() 恒成立,
恒成立,
令t=log2x,1≤t≤2,
即(t2)(![]() t
t![]() )≥mt对t∈[1,2]恒成立,
)≥mt对t∈[1,2]恒成立,
∴![]() 对t∈[1,2]恒成立,
对t∈[1,2]恒成立,
∵![]() ,当且仅当t=
,当且仅当t=![]() 时取等号,
时取等号,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|