题目内容
在三棱锥S-ABC中,AB⊥BC,AB=BC=
,SA=SC=2,二面角S-AC-B的余弦值是
,若S、A、B、C都在同一球面上,则该球的表面积是______.
| 2 |
| ||
| 3 |
如图所示:
取AC中点D,连接SD,BD,则由AB=BC,SA=SC得出SD⊥AC,BD⊥AC,
∴∠SDB为S-AC-B的平面角,且AC⊥面SBD.
由题意:AB⊥BC,AB=BC=
,易得:△ABC为等腰直角三角形,且AC=2,
又∵BD⊥AC,故BD=AD=
AC,
在△SBD中,BD=
AC=
×2=1,
在△SAC中,SD2=SA2-AD2=22-12=3,
在△SBD中,由余弦定理得SB2=SD2+BD2-2SD•BDcos∠SDB=3+1-2×
×1×
=2,
满足SB2=BD2=SD2,∴∠SBD=90°,SB⊥BD,
又SB⊥AC,BD∩AC=D,∴SB⊥面ABC.
以SB,BA,BC为顶点可以补成一个棱长为
的正方体,S、A、B、C都在正方体的外接球上,
正方体的对角线为球的一条直径,所以2R=
×
,R=
,球的表面积S=4π×
=6π.
故答案为:6π.
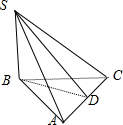
取AC中点D,连接SD,BD,则由AB=BC,SA=SC得出SD⊥AC,BD⊥AC,
∴∠SDB为S-AC-B的平面角,且AC⊥面SBD.
由题意:AB⊥BC,AB=BC=
| 2 |
又∵BD⊥AC,故BD=AD=
| 1 |
| 2 |
在△SBD中,BD=
| 1 |
| 2 |
| 1 |
| 2 |
在△SAC中,SD2=SA2-AD2=22-12=3,
在△SBD中,由余弦定理得SB2=SD2+BD2-2SD•BDcos∠SDB=3+1-2×
| 3 |
| ||
| 3 |
满足SB2=BD2=SD2,∴∠SBD=90°,SB⊥BD,
又SB⊥AC,BD∩AC=D,∴SB⊥面ABC.
以SB,BA,BC为顶点可以补成一个棱长为
| 2 |
正方体的对角线为球的一条直径,所以2R=
| 3 |
| 2 |
| ||
| 2 |
| 6 |
| 4 |
故答案为:6π.


练习册系列答案
相关题目