题目内容
20. 已知圆N:(x+1)2+y2=2和抛物线C:y2=x,圆N的切线l与抛物线C交于不同的两点A,B.
已知圆N:(x+1)2+y2=2和抛物线C:y2=x,圆N的切线l与抛物线C交于不同的两点A,B.(I)当切线l斜率为1时,求线段AB的长;
(Ⅱ)设点M和点N关于直线y=x对称,且$\overrightarrow{MA}•\overrightarrow{MB}=0$,求直线l的方程.
分析 (I)圆N的圆心N为(-1,0),半径r=$\sqrt{2}$,设A(x1,y1),B(x2,y2),设l的方程,利用直线l是圆N的切线,求得m的值,从而可得直线l的方程,与抛物线方程联立,利用韦达定理,即可计算弦长|AB|;
(Ⅱ)设直线l的方程为y=kx+m,由直线l是圆N的切线,得$\frac{|-k+m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$,解得此时直线l的方程为y=-x+1;当直线l的斜率不存在时,l的方程为x=$\sqrt{2}$-1则得不成立.综上所述,存在满足条件的直线l,其方程为y=-x+1.
解答 解:∵圆N:(x+1)2+y2=2,∴圆心N为(-1,0),半径r=$\sqrt{2}$,
设A(x1,y1),B(x2,y2),
(I)当直线l的斜率为1时,设l的方程为y=x+m,即x-y+m=0,
∵直线l是圆N的切线,∴$\frac{|-1+m|}{\sqrt{2}}$=$\sqrt{2}$,解得m=-1或m=3(舍),此时直线l的方程为y=x-1,
由直线与抛物线联立,消去x得y2-y-1=0,
∴△>0,y1+y2=1,y1y2=-1,
∴弦长|AB|=$\sqrt{1+1}$•$\sqrt{1+4}$=$\sqrt{10}$.
(Ⅱ)(i)设直线l的方程为y=kx+m,即kx-y+m=0(k≠0),
∵直线l是圆N的切线,∴$\frac{|-k+m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$,
得m2-k2-2mk-2=0,①
由直线与抛物线联立,消去x得ky2-y+m=0,
∴△=1-4k×m>0,即km<$\frac{1}{4}$且k≠0,y1+y2=$\frac{1}{k}$,y1y2=$\frac{m}{k}$,
∵点M与点N关于直线y=x对称,∴M(0,-1),
∴$\overrightarrow{MA}$=(x1,y1+1),$\overrightarrow{MB}$=(x2,y2+1),
∵$\overrightarrow{MA}•\overrightarrow{MB}=0$,∴x1x2+(y1+1)(y2+1)=0,
将A,B在直线y=kx+m上代入并化简,得
(1+k2)y1y2+(k2-m)(y1+y2)+m2+k2=0,
化简,得m2+k2+mk+k=0,②
①+②得2m2-mk+k-2=0,
即(m-1)(2m-k+2)=0,
解得m=1,或m=$\frac{1}{2}$k-1.
当m=1时,代入①,解得k=-1,满足条件km<$\frac{1}{4}$,且k≠0,
此时直线l的方程为y=-x+1.
当m=$\frac{1}{2}$k-1时,代入①整理,无解.
(ii)当直线l的斜率不存在时,
因为直线l是圆N的切线,所以l的方程为x=$\sqrt{2}$-1.
则得x1x2=3-2$\sqrt{2}$,y1+y2=0,
由①得:x1x2+(y1+1)(y2+1)
=x1x2+y1y2+(y1+y2)+1≠0,
当直线l的斜率不存在时,$\overrightarrow{MA}•\overrightarrow{MB}=0$不成立.
综上所述,存在满足条件的直线l,其方程为y=-x+1.
点评 本题考查线段长的求法,探索直线是否存在,具体涉及到圆的简单性质、抛物线的性质及其应用、直线与圆锥曲线的位置关系的应用.综合性强,难度大,是高考的重点.解题的关键是联立方程,正确运用韦达定理.

| A. | $\sqrt{2}$ | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2 |
| A. | $\sqrt{2}$π | B. | 2π | C. | 2$\sqrt{2}$π | D. | 4π |
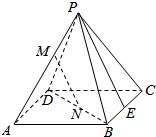 已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.
已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.