题目内容
15．若四面体SABC中，三组对棱分别相等，且长分别为$\sqrt{34}$，$\sqrt{41}$，5．则此四面体的体积为（ ）| A． | 20 | B． | 18 | C． | 16 | D． | 14 |
分析 由已知中四面体S-ABC三组对棱分别相等，且依次为$\sqrt{34}$，$\sqrt{41}$，5，故可将其补充为一个长方体，求出长方体的三边长，即可求出答案．
解答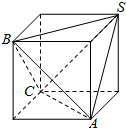 
解：∵四面体S-ABC三组对棱分别相等，且依次为$\sqrt{34}$，$\sqrt{41}$，5．
∴可将其补充为一个三个面上对角线长分别为$\sqrt{34}$，$\sqrt{41}$，5的长方体
∴长方体的三边长分别为3，4，5，
∴四面体的体积为5×3×4-4×$\frac{1}{3}$×$\frac{1}{2}$×5×3×4=20．
故选：A．
点评 本题考查的知识点是四面体的体积，其中利用割补法，补充四面体成长方体是解答本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
5．三棱锥的高为3，底面是边长为3的正三角形，则这个三棱锥的体积是（ ）
| A． | $\frac{27}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{27\sqrt{3}}{4}$ | D． | $\frac{9\sqrt{3}}{4}$ |
6．已知椭圆E：$\frac{x^2}{4}+\frac{y^2}{2}=1$，直线l交椭圆于A，B两点，若AB的中点坐标为（$\frac{1}{2}$，-1），则l的方程为（ ）
| A． | 2x+y=0 | B． | $x-2y-\frac{5}{2}=0$ | C． | 2x-y-2=0 | D． | $x-4y-\frac{9}{2}=0$ |
在几何体ABCDE中，∠BAC=$\frac{π}{2}$，DC⊥平面ABC，EB⊥平面ABC，AB=AC=BE=2，CD=1，设F是BC的中点．
4．
将某正方体工件进行切削，把它加工成一个体积尽可能大的新工件，新工件的三视图如图所示，则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕（ ）
将某正方体工件进行切削，把它加工成一个体积尽可能大的新工件，新工件的三视图如图所示，则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕（ ）| A． | $\frac{7}{8}$ | B． | $\frac{6}{7}$ | C． | $\frac{5}{6}$ | D． | $\frac{4}{5}$ |