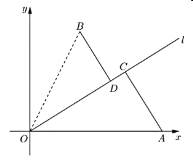
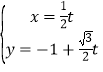题目内容
【题目】已知函数
，
.
（1）对任意的
，
成立，求实数
的取值范围；
（2）若
，证明：
.
【答案】(1) 
;(2)见解析.
【解析】
（1）解法一：构造函数
，求出
及
，然后分类讨论。
解法二：当
时，
恒成立；当
时，通过分离得到
，令
，转化为求在的最小值。
（2）由分析法要证
，即证：
继而由（1）的解法二知：
在时恒有
，得证.
(1)解法一：令
，
，
①当
时，对于任意的，
，
在
为增函数，
，
在为增函数，
，即，
恒成立，满足.
②当
时，令
，得
则当
时，为减函数，此时
，
故函数
为减函数，
，
即当时，有
，矛盾.
综上，实数
的取值范围是：
.
解法二：当时，恒成立；
当时，即为，
转化为求在的最小值，
，令
，
，
由
知：
在
为增函数，
故
在为增函数，
即
，函数
在为增函数，故没有最小值.
又由诺必达法则知：
，故.
（2）证明：要证，即证：，
，
，故即证：
，左边分子分母同除以
，
即证：
令
，则
，即证
，即证：
.
而由（1）的解法二知：在时恒有，得证.
练习册系列答案
相关题目
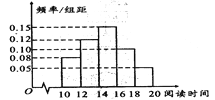
【题目】某教师将寒假期间该校所有学生阅读小说的时间统计如下图所示，并统计了部分学生阅读小说的类型，得到的数据如下表所示：
男生 | 女生 | |
阅读武侠小说 | 80 | 30 |
阅读都市小说 | 20 | 70 |
（1）是否有99.9%的把握认为“性别”与“阅读小说的类型”有关？
（2）求学生阅读小说时间的众数和平均数（同一组数据用该组区间的中点值作代表）；
（3）若按照分层抽样的方法从阅读时间在
、
的学生中随机抽取6人，再从这6人中随机挑选2人介绍选取小说类型的缘由，求所挑选的2人阅读时间都在的概率.
附：
，
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
