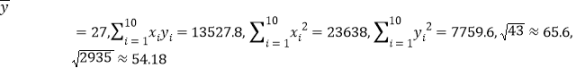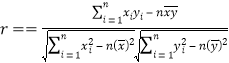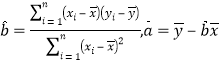ÌâÄżÄÚÈĘ
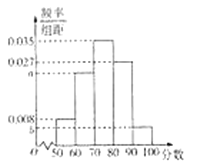
ĄŸÌâÄżĄżÊźŸĆŽóÒÔÀŽŁŹÄłÆ¶À§”ŰÇű·öƶ°ì»ęŒ«čáłčÂäÊ”čúŒÒŸ«ŚŒ·öƶ”ÄŐțČßÒȘÇóŁŹŽűÁìčăŽóĆ©Žć”ŰÇűÈËĂńÈșÖÚÍŃƶ±ŒĐĄż”ĄŁŸčęȻО”Ä·ÜÁŠÆŽČ«ŁŹĐÂĆ©ŽćœšÉèÈĄ”ĂŸȚŽóœűČœŁŹĆ©ĂńÄêÊŐÈëÒČÖđÄêÔöŒÓĄŁÎȘÁËžüșĂ”ÄÖƶš2019ÄêčŰÓÚŒÓżìÌáÉęĆ©ĂńÄêÊŐÈËÁŠŐùÔçÈŐÍŃƶ”Ä而śŒÆ»źŁŹžĂ”Ű·öƶ°ìÍłŒÆÁË2018Äê50λƩĂń”ÄÄêÊŐÈËČąÖÆłÉÈçÏÂÆ”ÂÊ·ÖČŒÖ±·œÍŒŁș
Łš1Ł©žùŸĘÆ”ÂÊ·ÖČŒÖ±·œÍŒŁŹčÀŒÆ50λƩĂń”ÄÄêÆœŸùÊŐÈë![]() Łš”„λŁșǧÔȘŁ©ŁšÍŹÒ»ŚéÊęŸĘÓÞÌéÊęŸĘÇűŒä”ÄÖĐ”ăÖ”±íÊŸŁ©Ł»
Łš”„λŁșǧÔȘŁ©ŁšÍŹÒ»ŚéÊęŸĘÓÞÌéÊęŸĘÇűŒä”ÄÖĐ”ăÖ”±íÊŸŁ©Ł»
Łš2Ł©ÓÉÆ”ÂÊ·ÖČŒÖ±·œÍŒŁŹżÉÒÔÈÏÎȘžĂƶÀ§”ŰÇűĆ©ĂńÄêÊŐÈë![]() ·țŽÓŐęÌŹ·ÖČŒ
·țŽÓŐęÌŹ·ÖČŒ![]() ŁŹÆäÖĐ
ŁŹÆäÖĐ![]() œüËÆÎȘÄêÆœŸùÊŐÈë
œüËÆÎȘÄêÆœŸùÊŐÈë![]() ,
,![]() œüËÆÎȘŃù±Ÿ·œČî
œüËÆÎȘŃù±Ÿ·œČî![]() ŁŹŸŒÆËă”Ă
ŁŹŸŒÆËă”Ă![]() .ÀûÓĂžĂŐęÌŹ·ÖČŒŁŹÇó:
.ÀûÓĂžĂŐęÌŹ·ÖČŒŁŹÇó:
(i)ÔÚ2019ÄêÍŃÆ¶č„Œá而śÖĐŁŹÈôÊčžĂ”ŰÇűÔŒÓĐŐŒŚÜĆ©ĂńÈËÊę”Ä![]() ”ÄĆ©Ăń”ÄÄêÊŐÈëžßÓÚ·öƶ°ìÖƶš”ÄŚî”ÍÄêÊŐÈë±êŚŒŁŹÔòŚî”ÍÄêÊŐÈëŽóÔŒÎȘ¶àÉÙǧÔȘŁż
”ÄĆ©Ăń”ÄÄêÊŐÈëžßÓÚ·öƶ°ìÖƶš”ÄŚî”ÍÄêÊŐÈë±êŚŒŁŹÔòŚî”ÍÄêÊŐÈëŽóÔŒÎȘ¶àÉÙǧÔȘŁż
ŁšiiŁ©ÎȘÁË”śŃĐĄ°Ÿ«ŚŒ·öƶŁŹČ»ÂäÒ»ÈËĄ±”ÄŐțČßÒȘÇóÂäÊ”Çéżö, ·öƶ°ìËæ»úŚß·ĂÁË1000λƩĂńĄŁÈôĂżžöĆ©Ăń”ÄÄêÊŐÈËÏໄ¶ÀÁąŁŹÎÊŁșŐâ1000λƩĂńÖĐ”ÄÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÈËÊęŚîÓĐżÉÄÜÊǶàÉÙŁż
žœŁșČÎżŒÊęŸĘÓëč«Êœ![]() ŁŹÈô
ŁŹÈô![]() Ą«
Ą«![]() ŁŹÔòąÙ
ŁŹÔòąÙ![]() Ł»ąÚ
Ł»ąÚ![]() Ł»ąÛ
Ł»ąÛ![]() .
.
ĄŸŽđ°žĄż(1)17.40ÍòÔȘ (2) (i) 14.77ǧÔȘ ŁšiiŁ©978
ĄŸœâÎöĄż
Łš1Ł©ÓÉĂżÒ»žöĐĄŸŰĐÎÖĐ”ă”ÄșáŚű±êłËÒÔÆ”ÂÊŚśș͔Î𰞣»
Łš2Ł©ÓÉÌâÒ⣏XĄ«NŁš17.40ŁŹ6.92Ł©ŁŹŁź
ŁšiŁ©ÓÉÒŃÖȘÊęŸĘÇó”ĂPŁšxŁŸŠÌ©ŠÒŁ©ŁŹœűÒ»ČœÇó”ĂŠÌ©ŠÒ”Î𰞣»
ŁšąąŁ©ÇółöPŁšXĄĘ12.14Ł©ŁŹ”ĂĂżžöĆ©ĂńÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÊÂŒțžĆÂÊÎȘ0.9773ŁŹÉè1000žöĆ©ĂńÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÈËÊęÎȘŠÎŁŹÔòŠÎĄ«BŁš103ŁŹpŁ©ŁŹÇółöÇĄșĂÓĐkžöĆ©Ăń”ÄÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÊÂŒțžĆÂÊŁŹÓÉ![]() 1ŁŹ”ĂkŁŒ1001pŁŹœáșÏ1001pŁœ978.233ŁŹ¶Ôk·ÖÀà·ÖÎö”Î𰞣ź
1ŁŹ”ĂkŁŒ1001pŁŹœáșÏ1001pŁœ978.233ŁŹ¶Ôk·ÖÀà·ÖÎö”Î𰞣ź
œâŁșŁš1Ł©![]() ǧÔȘ.
ǧÔȘ.
Łš2Ł©ÓĐÌâÒ⣏![]() Ą«
Ą«![]() .
.
ŁšiŁ©![]()
![]() ʱŁŹÂúŚăÌâÒâ
ʱŁŹÂúŚăÌâÒâ
ŒŽŚî”ÍÄêÊŐÈëŽóÔŒÎȘ14.77ǧÔȘ
ŁšiiŁ©ÓÉ![]() ŁŹ”Ă
ŁŹ”Ă
ĂżžöĆ©Ăń”ÄÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÊÂŒțžĆÂÊÎȘ0.9773ŁŹ
ŒÇ1000žöĆ©Ăń”ÄÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÈËÊęÎȘ![]() ŁŹÔò
ŁŹÔò![]() ŁŹÆäÖĐ
ŁŹÆäÖĐ![]() ŁŹ
ŁŹ
ÓÚÊÇÇĄșĂÓĐ![]() žöĆ©Ăń”ÄÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÊÂŒțžĆÂÊÊÇ
žöĆ©Ăń”ÄÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÊÂŒțžĆÂÊÊÇ![]()
ŽÓ¶űÓÉ![]() ŁŹ”Ă
ŁŹ”Ă![]()
¶ű![]() ŁŹËùÒÔŁŹ
ŁŹËùÒÔŁŹ
”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ
ŁŹ
”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ
ŁŹ
ÓÉŽËżÉÖȘŁŹÔÚËùŚß·Ă”Ä1000λƩĂńÖĐŁŹÄêÊŐÈëČ»ÉÙÓÚ12.14ǧÔȘ”ÄÈËÊęŚîÓĐżÉÄÜÊÇ978

 Ìá·Ö°Ù·Ö°ÙŒìČâŸí”„ÔȘÆÚÄ©ČâÊÔŸíÏ”ÁĐŽđ°ž
Ìá·Ö°Ù·Ö°ÙŒìČâŸí”„ÔȘÆÚÄ©ČâÊÔŸíÏ”ÁĐŽđ°ž