题目内容
12.设F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,P是双曲线右支上一点,满足($\overrightarrow{OP}+\overrightarrow{O{F}_{2}}$)$•\overrightarrow{P{F}_{2}}$=0(O为坐标原点),且3|$\overrightarrow{P{F}_{1}}$|=4|$\overrightarrow{P{F}_{2}}$|,则双曲线的离心率为5.分析 运用双曲线的定义,结合条件可得|PF1|=8a,|PF2|=6a,再由($\overrightarrow{OP}+\overrightarrow{O{F}_{2}}$)$•\overrightarrow{P{F}_{2}}$=0,可得|OP|=|OF2|,得到∠F1PF2=90°,由勾股定理及离心率公式,计算即可得到.
解答 解:由于点P在双曲线的右支上,
则由双曲线的定义可得|PF1|-|PF2|=2a,
又|PF1|=$\frac{4}{3}$|PF2|,
解得|PF1|=8a,|PF2|=6a,
由($\overrightarrow{OP}+\overrightarrow{O{F}_{2}}$)$•\overrightarrow{P{F}_{2}}$=0,
即为($\overrightarrow{OP}+\overrightarrow{O{F}_{2}}$)•($\overrightarrow{O{F}_{2}}$-$\overrightarrow{OP}$)=0,
即有$\overrightarrow{OP}$2=$\overrightarrow{O{F}_{2}}$2,
则△PF1F2中,|OP|=|OF2|=|OF1|,
则∠F1PF2=90°,
由勾股定理得|PF1|2+|PF2|2=|F1F2|2,
即有64a2+36a2=4c2,
即有c=5a,
即e=$\frac{c}{a}$=5.
故答案为:5
点评 本题考查双曲线的定义、方程和性质,考查双曲线的离心率的求法,同时考查向量垂直的条件和勾股定理的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
7.已知偶函数f(x)在[0,+∞)上单调递增,且f(a+1)>f(a-1),则示数a的取值范围是( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-1,+∞) |
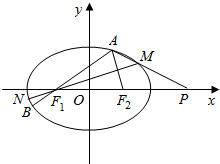 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$.A为椭圆C上一动点(A异于左、右顶点),F1、F2分别为椭圆C的左、右焦点,且△AF1F2面积的最大值为1;
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$.A为椭圆C上一动点(A异于左、右顶点),F1、F2分别为椭圆C的左、右焦点,且△AF1F2面积的最大值为1;