题目内容
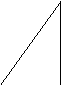
下面的一组图形为某一四棱锥S-ABCD的侧面与底面。
 | |||||
 |  | ||||
![]()
![]()
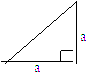 | 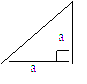 | ||||||
(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA![]() 面ABCD,E为AB中点,求二面角E-SC-D的大小;
面ABCD,E为AB中点,求二面角E-SC-D的大小;
(3)求点D到面SEC的距离。
(1)存在一条侧棱垂直于底面(2)二面角E-SC-D的大小为90![]() (3)点D到面SEC的距离为
(3)点D到面SEC的距离为![]()
解析:
(1)存在一条侧棱垂直于底面(如图)

![]() 且AB、AD是面ABCD内的交线
且AB、AD是面ABCD内的交线![]() SA
SA![]() 底面ABCD
底面ABCD
(2)分别取SC、SD的中点G、F,连GE、GF、FA,
则GF//EA,GF=EA,![]() AF//EG
AF//EG
而由SA![]() 面ABCD得SA
面ABCD得SA![]() CD,
CD,
又AD![]() CD,
CD,![]() CD
CD![]() 面SAD,
面SAD,![]()
又SA=AD,F是中点,![]()
![]() 面SCD,EG
面SCD,EG![]() 面SCD,
面SCD,![]() 面SCD
面SCD
所以二面角E-SC-D的大小为90![]()
(3)作DH![]() SC于H,
SC于H,
![]() 面SEC
面SEC![]() 面SCD,
面SCD,![]() DH
DH![]() 面SEC,
面SEC,
![]() DH之长即为点D到面SEC的距离,12分
DH之长即为点D到面SEC的距离,12分
![]() 在Rt
在Rt![]() SCD中,
SCD中,![]()
答:点D到面SEC的距离为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

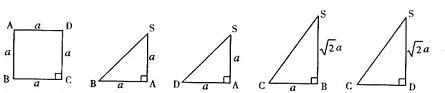
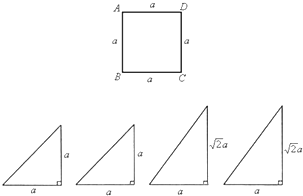 (2006•宣武区一模)下面的一组图形为某一四棱锥S-ABCD的侧面与底面.
(2006•宣武区一模)下面的一组图形为某一四棱锥S-ABCD的侧面与底面.