题目内容
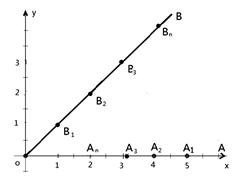
平面直角坐标系中, 为原点,射线
为原点,射线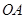 与
与 轴正半轴重合,射线
轴正半轴重合,射线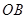 是第一象限角平分线.在
是第一象限角平分线.在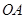 上有点列
上有点列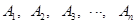 ,
,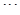 ,在
,在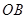 上有点列
上有点列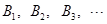 ,
,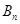 ,
,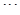 .已知
.已知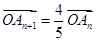 ,
,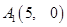 ,
,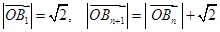 .
.
(1)求点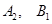 的坐标;
的坐标;
(2)求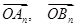 的坐标;
的坐标;
(3)求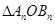 面积的最大值,并说明理由.
面积的最大值,并说明理由.
(1)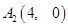 ,
,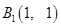 ;(2)
;(2)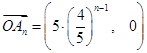 ,
,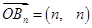 ;(3)
;(3)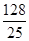 ;
;
解析试题分析:(1)由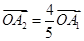 和
和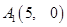 可求
可求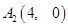 ,由射线
,由射线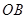 是第一象限角平分线和
是第一象限角平分线和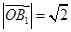 ,利用向量模的公式可求
,利用向量模的公式可求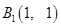 ;(2)设
;(2)设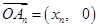 ,
,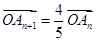 可得
可得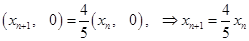
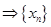 成等比数列,又
成等比数列,又 得
得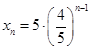 ,进而得到
,进而得到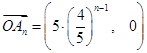 ;设
;设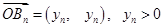 ,得
,得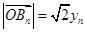 ,由
,由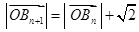 ,得
,得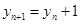 得
得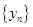 是等差数列,可求得
是等差数列,可求得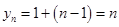 ,进而求得
,进而求得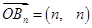 ;(3)由
;(3)由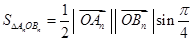 ,可得
,可得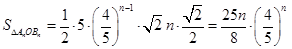 ,利用换元法设
,利用换元法设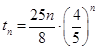 ,当
,当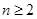 时,
时, 可知
可知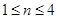 时,
时,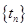 是递增数列,
是递增数列,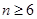 时,
时,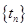 是递减数列,即
是递减数列,即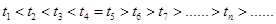 进而求得
进而求得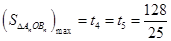 ;
;
试题解析:(1)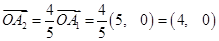 ,
, 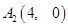 , 2分
, 2分
设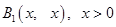 ,由
,由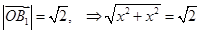 ,
,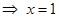 ,∴
,∴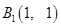 ; 4分
; 4分
(2)设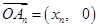 ,则
,则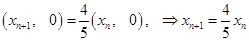 ,
,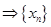 成等比数列, 5分
成等比数列, 5分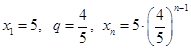 ,∴
,∴ 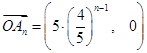 ; 6分
; 6分
设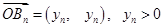 ,
,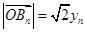 , 7分
, 7分
由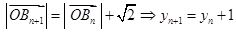 ,
,
∴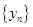 是等差数列, 8分
是等差数列, 8分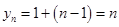 , ∴
, ∴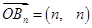 . 9分
. 9分
(3)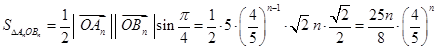 , 11分
, 11分
设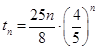 ,
,
当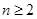 时,
时,
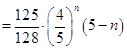 , 12分
, 12分
∴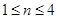 时,
时,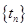 是递增数列,
是递增数列,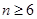 时,
时,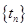 是递减数列,
是递减数列,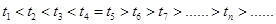 , 13分
, 13分
∴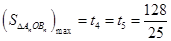 .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知数列 的前n项和
的前n项和 ,则( )
,则( )
A. 是递增的等比数列 是递增的等比数列 | B. 是递增数列,但不是等比数列 是递增数列,但不是等比数列 |
C. 是递减的等比数列 是递减的等比数列 | D. 不是等比数列,也不单调 不是等比数列,也不单调 |
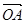 =(5,1),
=(5,1),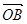 =(1,7),
=(1,7), =(4,2),且
=(4,2),且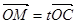 .
.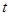 ,使
,使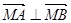 ?若存在,求出实数
?若存在,求出实数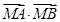 取最小值点M的坐标.
取最小值点M的坐标.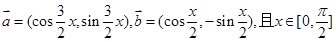 ,
,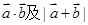 ;
; 的最小值是
的最小值是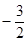 ,求实数
,求实数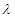 的值.
的值.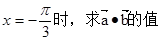 ;(2)求|a+b|的最大值
;(2)求|a+b|的最大值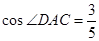 ,
,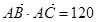 .
.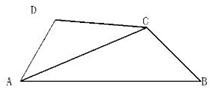
 ;
; ,求x、y的值。
,求x、y的值。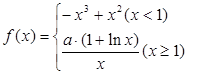 ,曲线
,曲线 上是否存在两点
上是否存在两点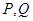 ,使得△
,使得△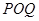 是以
是以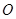 为直角顶点的直角三角形,且此三角形斜边的中点在
为直角顶点的直角三角形,且此三角形斜边的中点在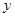 轴上.如果存在,求出实数
轴上.如果存在,求出实数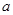 的范围;如果不存在,说明理由.
的范围;如果不存在,说明理由.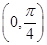 .
.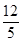 ,求sin
,求sin 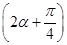 的值.
的值.