题目内容
已知函数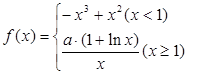 ,曲线
,曲线 上是否存在两点
上是否存在两点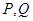 ,使得△
,使得△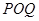 是以
是以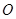 为直角顶点的直角三角形,且此三角形斜边的中点在
为直角顶点的直角三角形,且此三角形斜边的中点在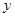 轴上.如果存在,求出实数
轴上.如果存在,求出实数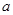 的范围;如果不存在,说明理由.
的范围;如果不存在,说明理由.
存在,且实数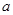 的取值范围是
的取值范围是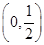 .
.
解析试题分析:先将斜边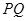 的中点在
的中点在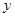 轴上这一条件进行转化,确定点
轴上这一条件进行转化,确定点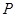 与点
与点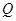 之间的关系,并将
之间的关系,并将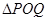 是以点
是以点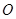 为直角顶点条件转化为
为直角顶点条件转化为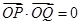 ,进行得到一个方程,然后就这个方程在定义域上是否有解对自变量的取值进行分类讨论,进而求出参数
,进行得到一个方程,然后就这个方程在定义域上是否有解对自变量的取值进行分类讨论,进而求出参数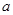 的取值范围.
的取值范围.
试题解析:假设曲线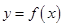 上存在两点
上存在两点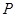 、
、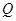 满足题意,则
满足题意,则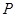 、
、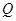 两点只能在
两点只能在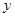 轴两侧,
轴两侧,
因为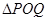 是以
是以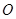 为直角顶点的直角三角形,所以
为直角顶点的直角三角形,所以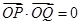 ,
,
不妨设 ,则由
,则由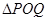 的斜边的中点在
的斜边的中点在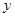 轴上知
轴上知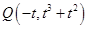 ,且
,且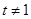 ,
,
由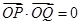 ,所以
,所以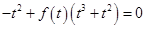 (*)
(*)
是否存在两点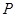 、
、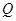 满足题意等价于方程(*)是否有解问题,
满足题意等价于方程(*)是否有解问题,
(1)当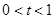 时,即
时,即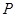 、
、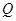 都在
都在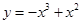 上,则
上,则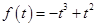 ,
,
代入方程(*),得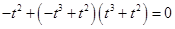 ,即
,即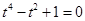 ,而此方程无实数解;
,而此方程无实数解;
(2)当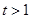 时,即
时,即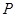 在
在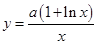 上,
上,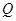 在
在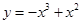 上,
上,
则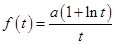 ,代入方程(*)得,
,代入方程(*)得,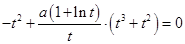 ,即
,即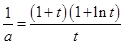 ,
,
设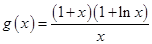 ,则
,则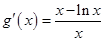 ,
,
再设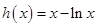 ,则
,则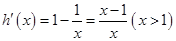 ,所以
,所以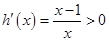 在
在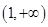 上恒成立,
上恒成立,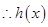 在
在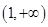 上单调递增,
上单调递增,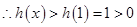 ,从而
,从而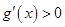 ,故
,故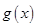 在
在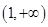 上也单调递增,
上也单调递增,
所以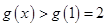 ,即
,即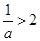 ,解得
,解得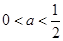 ,
,
即当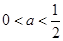 时,方程
时,方程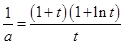 有解,即方程(*)有解,
有解,即方程(*)有解,
所以曲线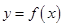 上总存在两点
上总存在两点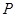 、
、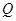 ,使得
,使得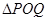 是以
是以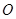 为直角顶点的直角三角形,
为直角顶点的直角三角形,
且此三角形斜边的中点在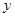 轴上,此时
轴上,此时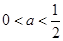 .
.
考点:1.平面向量垂直;2.函数的零点

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知数列2,5,11,20,x,47, 合情推出x的值为( )
| A.29 | B.31 | C.32 | D.33 |
下列四个数中,哪一个是数列{ }中的一项 ( )
}中的一项 ( )
| A.380 | B.39 | C.35 | D.23 |
已知数列的通项公式是 ,则
,则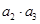 等于( )
等于( )
| A.70 | B.28 | C.20 | D.8 |
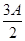 ,sin
,sin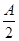 ,sin
,sin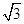 .
.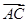 |+|
|+| |=
|=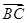 |,试判断△ABC的形状.
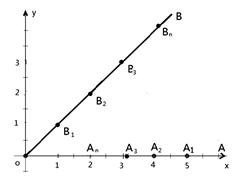
|,试判断△ABC的形状. 为原点,射线
为原点,射线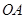 与
与 轴正半轴重合,射线
轴正半轴重合,射线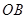 是第一象限角平分线.在
是第一象限角平分线.在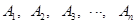 ,
,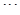 ,在
,在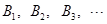 ,
,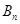 ,
,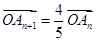 ,
,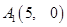 ,
,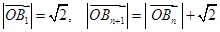 .
.
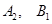 的坐标;
的坐标;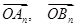 的坐标;
的坐标;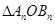 面积的最大值,并说明理由.
面积的最大值,并说明理由.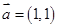 ,
,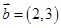 ,当
,当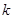 为何值时,
为何值时,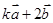 与
与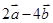 垂直?
垂直?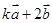 与
与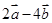 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?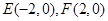 ,曲线
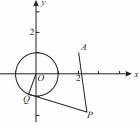
,曲线 上的动点
上的动点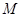 满足
满足 ,定点
,定点 ,由曲线
,由曲线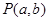 向曲线
向曲线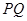 ,切点为
,切点为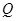 ,且满足
,且满足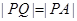 .
.
 为圆心所作的圆
为圆心所作的圆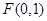 是中心在坐标原点
是中心在坐标原点 的椭圆
的椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆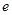 为
为 .
.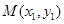 、
、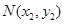 为椭圆
为椭圆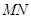 的斜率为
的斜率为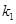 ;
; 是满足
是满足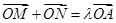 (
(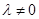 )的点,且直线
)的点,且直线 的斜率为
的斜率为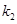 .
.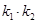 的值;
的值;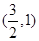 ,求实数
,求实数 的取值范围.
的取值范围.