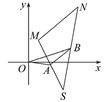
题目内容
设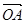 =(5,1),
=(5,1),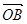 =(1,7),
=(1,7), =(4,2),且
=(4,2),且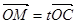 .
.
(1)是否存在实数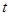 ,使
,使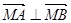 ?若存在,求出实数
?若存在,求出实数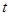 ;若不存在,请说明理由;
;若不存在,请说明理由;
(2)求使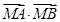 取最小值点M的坐标.
取最小值点M的坐标.
(1) ;(2)
;(2) .
.
解析试题分析:解题思路:(1)用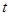 表示
表示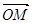 ,利用
,利用 得到关于
得到关于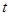 的方程即可;(2)借助(1)中
的方程即可;(2)借助(1)中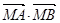 关于
关于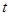 的一元二次函数求最值.规律总结:平面向量的坐标运算的关键要利用向量共线得出相关点的坐标,再进行求解;一定要记住平面向量平行、垂直的充要条件.
的一元二次函数求最值.规律总结:平面向量的坐标运算的关键要利用向量共线得出相关点的坐标,再进行求解;一定要记住平面向量平行、垂直的充要条件.
试题解析:(1)设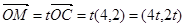 ,
, ,
, ,
, ,
, ,
, ,
,
即 ,解得
,解得 .
.
由(1)得, ,
,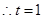 时,
时, ,此时
,此时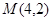 .
.
考点:平面向量共线、平面向量数量积运算.

练习册系列答案
相关题目
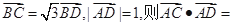 ________.
________. 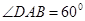 ,E、F分别为CD,BC的中点,则
,E、F分别为CD,BC的中点,则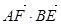 =
= 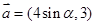 ,
,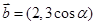 ,且
,且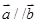 ,则锐角
,则锐角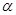 为________.
为________.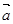 =(2,3),
=(2,3), =(﹣1,2)当k为何值时,
=(﹣1,2)当k为何值时,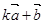 与
与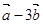 垂直?
垂直?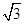 cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+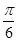 ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n. ·
· =
=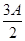 ,sin
,sin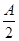 ,sin
,sin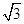 .
.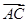 |+|
|+| |=
|=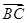 |,试判断△ABC的形状.
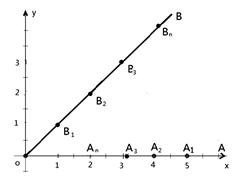
|,试判断△ABC的形状. 为原点,射线
为原点,射线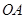 与
与 轴正半轴重合,射线
轴正半轴重合,射线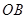 是第一象限角平分线.在
是第一象限角平分线.在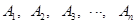 ,
,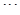 ,在
,在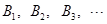 ,
,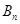 ,
,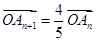 ,
,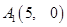 ,
,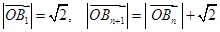 .
.
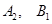 的坐标;
的坐标;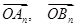 的坐标;
的坐标;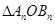 面积的最大值,并说明理由.
面积的最大值,并说明理由. =a,
=a, =b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若
=b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若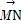 ⊥(λa+b),则实数λ= .
⊥(λa+b),则实数λ= .