题目内容
:数列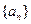 满足:
满足: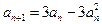 ,
,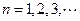 .
.
(Ⅰ)若数列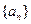 为常数列,求
为常数列,求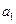 的值;
的值;
(Ⅱ)若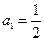 ,求证:
,求证: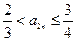 ;(Ⅲ)在(Ⅱ)的条件下,求证:数列
;(Ⅲ)在(Ⅱ)的条件下,求证:数列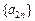 单调递减.
单调递减.
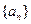 满足:
满足: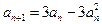 ,
,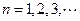 .
.(Ⅰ)若数列
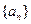 为常数列,求
为常数列,求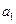 的值;
的值;(Ⅱ)若
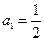 ,求证:
,求证: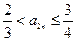 ;(Ⅲ)在(Ⅱ)的条件下,求证:数列
;(Ⅲ)在(Ⅱ)的条件下,求证:数列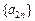 单调递减.
单调递减.:略
:解:(Ⅰ)因为数列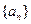 为常数列,
为常数列,
所以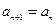 ,
,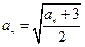
解得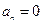 或
或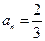
由 的任意性知,
的任意性知,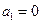 或
或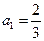 .
.
所以 ,
,
或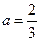 . ………………… 3 分
. ………………… 3 分
(Ⅱ)用数学归纳法证明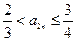 .
.
① 当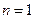 时,
时,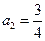 ,
,
符合上式. ………………… 4 分
② 假设当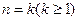 时,
时,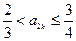 ,
,
因为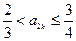 ,
,
所以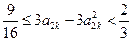 ,即
,即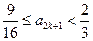 .
.
从而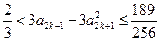 ,即
,即 .
.
因为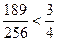 ,
,
所以,当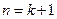 时,
时, 成立.
成立.
由①,②知,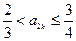 . ………………… 9分
. ………………… 9分
(Ⅲ)因为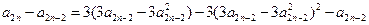
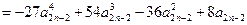 (
(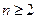 ),
),
所以只要证明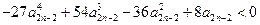 .
.
由(Ⅱ)可知,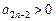 ,
,
所以只要证明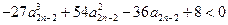 ,
,
即只要证明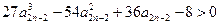 . …………………12分
. …………………12分
令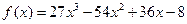 ,
,
 ,
,
所以函数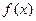 在
在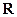 上单调递增. ………………… 14分
上单调递增. ………………… 14分
因为 ,
,
所以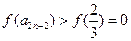 ,即
,即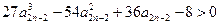 成立.
成立.
故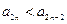 .
.
所以数列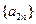 单调递减. ………………… 16分
单调递减. ………………… 16分
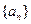 为常数列,
为常数列,所以
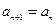 ,
,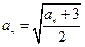
解得
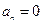 或
或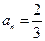
由
 的任意性知,
的任意性知,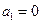 或
或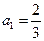 .
.所以
 ,
,或
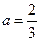 . ………………… 3 分
. ………………… 3 分(Ⅱ)用数学归纳法证明
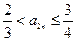 .
.① 当
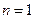 时,
时,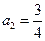 ,
,符合上式. ………………… 4 分
② 假设当
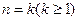 时,
时,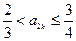 ,
,因为
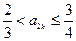 ,
,所以
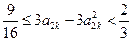 ,即
,即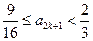 .
.从而
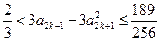 ,即
,即 .
.因为
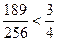 ,
,所以,当
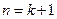 时,
时, 成立.
成立.由①,②知,
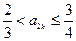 . ………………… 9分
. ………………… 9分(Ⅲ)因为
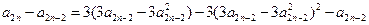
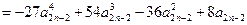 (
(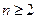 ),
),所以只要证明
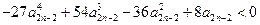 .
.由(Ⅱ)可知,
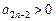 ,
,所以只要证明
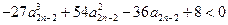 ,
,即只要证明
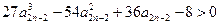 . …………………12分
. …………………12分令
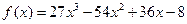 ,
, ,
,所以函数
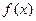 在
在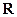 上单调递增. ………………… 14分
上单调递增. ………………… 14分因为
 ,
,所以
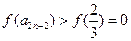 ,即
,即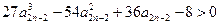 成立.
成立.故
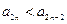 .
.所以数列
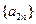 单调递减. ………………… 16分
单调递减. ………………… 16分
练习册系列答案
相关题目
 列
列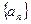 满足
满足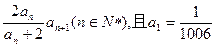 。
。 求证:数列
求证:数列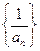 是等差数列,并求通项
是等差数列,并求通项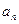 ;
;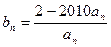 ,且
,且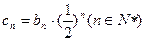 ,求和
,求和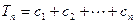 ;
;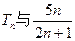 的大小,并予以证明。
的大小,并予以证明。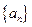 的前
的前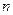 项和是
项和是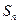 ,且
,且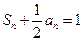 .
.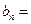
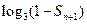 ,求适合方程
,求适合方程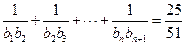 的
的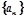 是公差不为0的等差数列,
是公差不为0的等差数列,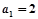 且
且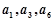 成等比数列,则
成等比数列,则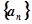 的前
的前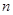 项和
项和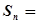
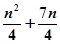
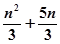
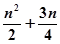
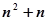
 数列
数列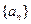 中,若
中,若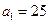 且
且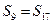 .
.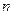 项和的最大值及取得最大值时相应的
项和的最大值及取得最大值时相应的 序号
序号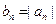 ,求数列
,求数列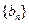 的前
的前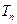
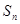 是等差数列
是等差数列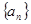 的前
的前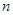 项和,若
项和,若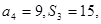 ,则数列
,则数列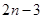
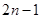
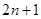
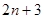
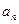 }中,
}中,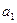 =
=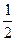 ,
,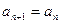 +
+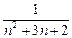 (n
(n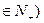 ,则
,则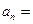 ( )
( )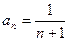
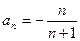
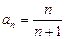
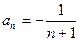
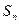 是等比数列{
是等比数列{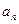 }的前
}的前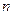 项和,
项和, 2,
2,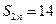 ,则
,则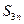 为 ( )
为 ( ) 的前5项和
的前5项和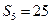 ,且
,且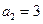 ,则
,则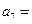 ( )
( )