题目内容
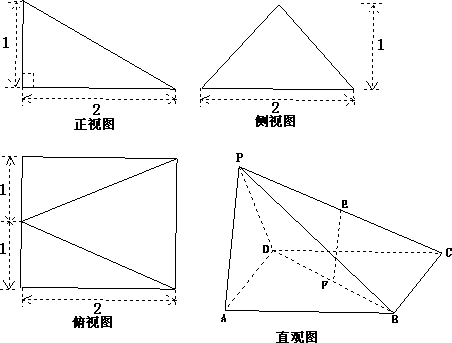
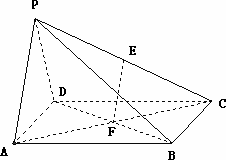
如图,多面体PABCD的直观图及三视图如图所示,E、F分别为PC、BD的中点.
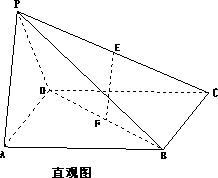
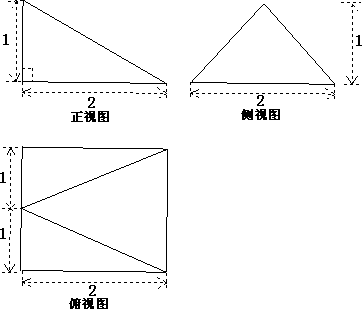
(1)求证:EF∥平面PAD;
(2)求证:平面PDC⊥平面PAD.
答案:
解析:
解析:
证明:由多面体PABCD的三视图知,四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是等腰三角形,![]() ,
,
且平面PAD⊥平面ABCD 2分
(1)连结AC,则F是AC的中点,在△CPA中,EF∥PA 4分
且PA![]() 平面PAD,EF
平面PAD,EF![]() 平面PAD,
平面PAD,
∴EF∥平面PAD 6分

(2)因为平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
又CD⊥AD,所以,CD⊥平面PAD,
∴CD⊥PA 8分
又![]() ,AD=2,所以△PAD是等腰直角三角形,
,AD=2,所以△PAD是等腰直角三角形,
且![]() ,即PA⊥PD 10分
,即PA⊥PD 10分
又CD∩PD=D,
∴PA⊥平面PDC,
又PA![]() 平面PAD,
平面PAD,
所以平面PAD⊥平面PDC 12分

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
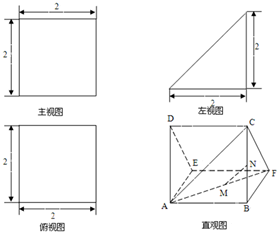 如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.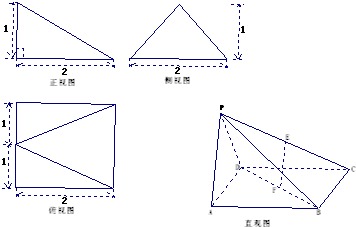
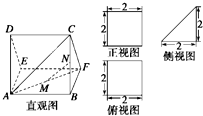 如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.