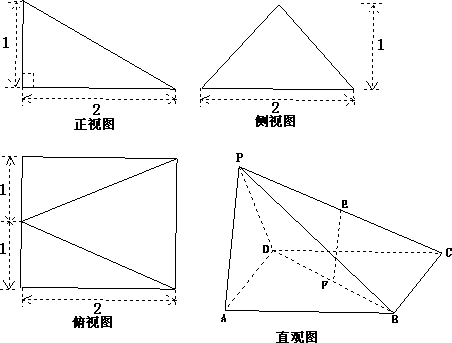
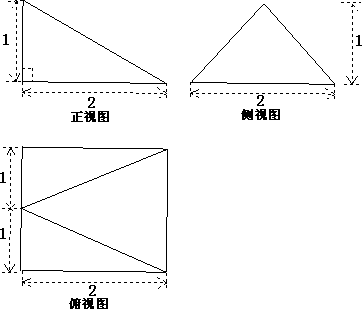
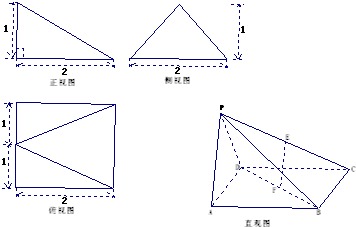
题目内容
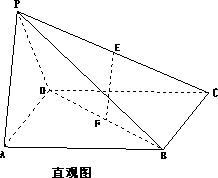
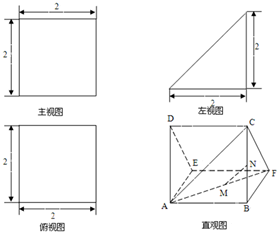
如图,多面体PABCD的直观图及三视图如图所示,E、F分别为PC、BD的中点.
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)求证:平面PDC⊥平面PAD.
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)求证:平面PDC⊥平面PAD.

分析:(Ⅰ)直接由线面平行的判定定理证明EF∥平面PAD;
(Ⅱ)要证平面PDC⊥平面PAD,只需证明平面PDC垂直于平面PAD内的一条垂涎即可,有面面垂直的性质及解直角三角形即可得到证明.
(Ⅱ)要证平面PDC⊥平面PAD,只需证明平面PDC垂直于平面PAD内的一条垂涎即可,有面面垂直的性质及解直角三角形即可得到证明.
解答: 证明:由多面体PABCD的三视图知,四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是等腰三角形,PA=PD=
证明:由多面体PABCD的三视图知,四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是等腰三角形,PA=PD=
,
且平面PAD平面ABCD.
(1)连结AC,则F是AC的中点,
在△CPA中,EF∥PA,
且PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD;
(2)因为平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
又CD⊥AD,所以,CD⊥平面PAD,
∴CD⊥PA
又PA=AD=
,AD=2,∴△PAD是等腰直角三角形,
且∠PAD=
,即PA⊥AD
又CD∩PD=D,∴PA⊥平面PDC,
又PA?平面PAD,
∴平面PAD⊥平面PDC.
 证明:由多面体PABCD的三视图知,四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是等腰三角形,PA=PD=
证明:由多面体PABCD的三视图知,四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是等腰三角形,PA=PD=| 2 |
且平面PAD平面ABCD.
(1)连结AC,则F是AC的中点,
在△CPA中,EF∥PA,
且PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD;
(2)因为平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
又CD⊥AD,所以,CD⊥平面PAD,
∴CD⊥PA
又PA=AD=
| 2 |
且∠PAD=
| π |
| 2 |
又CD∩PD=D,∴PA⊥平面PDC,
又PA?平面PAD,
∴平面PAD⊥平面PDC.
点评:本题考查了面面垂直的判定,考查了直线与平面垂直的性质,综合考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
 如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.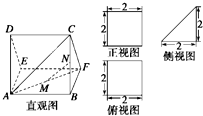 如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.