题目内容
与向量
 的夹角相等,且模为1的向量是 ( )
的夹角相等,且模为1的向量是 ( )
A. | B. 或 或 |
C. | D. 或 或 |
B
解析试题分析:因为|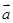 |=|
|=|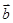 |,所以由向量的平行四边形法则,
|,所以由向量的平行四边形法则,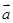 +
+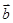 平分
平分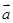 ,
,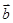 夹角。所以所求向量与
夹角。所以所求向量与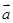 +
+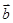 平行。
平行。
而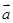 +
+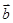 ="(4,-3)," 因此所求单位向量为
="(4,-3)," 因此所求单位向量为 或
或 ,选B。
,选B。
考点:本题主要考查平面向量的坐标运算,平面向量夹角的概念。
点评:基础题,向量是既有大小又有方向的量,因此,确定向量要确定其模和方向。利用坐标运算,通过解方程(组)也可使问题得解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各组向量:① 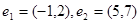 ;②
;②  ;
;
③ ,能作为表示它们所在平面内所有向量的基底的是( )
,能作为表示它们所在平面内所有向量的基底的是( )
| A.① | B.①③ | C.②③ | D.①②③ |
设 ,
, ,
, 为坐标平面上三点,
为坐标平面上三点, 为坐标原点,若
为坐标原点,若 与
与 在
在 方向上的投影相同,则
方向上的投影相同,则 与
与 满足的关系式为( )
满足的关系式为( )
A. | B. | C. | D. |
已知A(7,8),B(3,5),则向量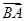 方向上的单位向量的坐标是 ( )
方向上的单位向量的坐标是 ( )
A.(- ,- ,- ) ) | B.( , , ) ) | C.( , , ) ) | D.(4,3) |
以下说法错误的是 ( )
A.直角坐标平面内直线的倾斜角的取值范围是 |
B.直角坐标平面内两条直线夹角的取值范围是 |
C.平面内两个非零向量的夹角的取值范围是 |
D.空间两条直线所成角的取值范围是 |
若三点 共线,则有( )
共线,则有( )
A. | B. | C. | D. |
已知 ,
, ,则下列结论正确的是
,则下列结论正确的是
A. ∥ ∥  | B. |
C. 与 与 垂直 垂直 | D. 与 与 的夹角为 的夹角为 |
设向量 ,
,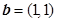 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. | C.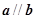 | D. |
设向量
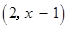 ,
,
 ,则“
,则“ ”是“
”是“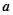 //
// ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |