题目内容
若三点 共线,则有( )
共线,则有( )
A. | B. | C. | D. |
C
解析试题分析:因为三点 ,所以
,所以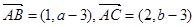 ,又三点
,又三点 共线,所以
共线,所以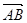 //
//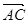 ,所以
,所以 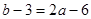 即
即 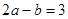 .
.
考点:向量的共线定理
点评:本题考查向量坐标的求法、考查向量共线定理得坐标形式的充要条件:坐标交叉相乘相等.

练习册系列答案
相关题目
在 中,
中, ,
, .若点D满足
.若点D满足 ,则
,则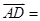 ( )
( )
A. | B. | C. | D. |
已知△ABC和点M满足 .若存在实数m使得
.若存在实数m使得 成立,则m=( )
成立,则m=( )
| A.2 | B.3 | C.4 | D.5 |
与向量
 的夹角相等,且模为1的向量是 ( )
的夹角相等,且模为1的向量是 ( )
A. | B. 或 或 |
C. | D. 或 或 |
若 是非零向量且满足
是非零向量且满足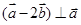 ,
, ,则
,则 与
与 的夹角是( )
的夹角是( )
A. | B. | C. | D. |
已知 =(5,-3),C(-1,3),
=(5,-3),C(-1,3), =2
=2 ,则点D的坐标为
,则点D的坐标为
| A.(11,9) | B.(4,0) | C.(9, 3) | D.(9,-3) |
已知向量 且
且 ,则实数x等于 ( )
,则实数x等于 ( )
A. | B. 9 | C. 4 | D. -4 |
已知平面向量 与
与 的夹角为60o,且满足
的夹角为60o,且满足 ,若
,若 =1,则
=1,则 =( )
=( )
| A.2 | B. | C.1 | D. |



