题目内容
8.已知定义域为R的奇函数f(x)满足:当x∈(0,+∞)时,f(x)=x(x+2).(1)求f(x)的解析式,并讨论f(x)的单调性;
(2)若实数x满足f(x2-bx)<f($\frac{x-b}{2}$),其中常数b∈R,试求实数x的取值范围.
分析 (1)根据函数奇偶性的性质即可求f(x)的解析式,利用数形结合即可判断f(x)的单调性;
(2)格局函数单调性的性质将不等式进行转化,利用一元二次不等式的解法进行求解即可.
解答  解:(1)当-x∈(-∞,0),则-x∈(0,+∞),
解:(1)当-x∈(-∞,0),则-x∈(0,+∞),
∵当x∈(0,+∞)时,f(x)=x(x+2).
∴当-x∈(0,+∞)时,f(-x)=-x(-x+2).
∵f(x)是奇函数,
∴f(-x)=-x(-x+2)=-f(x).
即f(x)=-x(x-2),
当x=0时,f(0)=0,
f(x)=$\left\{\begin{array}{l}{x(x+2),}&{x≥0}\\{-x(x-2),}&{x<0}\end{array}\right.$,
作出函数f(x)的图象,则函数f(x)为增函数.
(2)∵f(x)为增函数,
∴由f(x2-bx)<f($\frac{x-b}{2}$),
得x2-bx<$\frac{x-b}{2}$,
即2x2-2bx<x-b,
即2x2-(2b+1)x+b<0,
即(x-b)(2x-1)<0,
则2(x-b)(x-$\frac{1}{2}$)<0,
若b=$\frac{1}{2}$,则不等式等价为(x-$\frac{1}{2}$)2<0,此时不等式无解,
若b>$\frac{1}{2}$,则不等式的解为$\frac{1}{2}$<x<b,
若b<$\frac{1}{2}$,则不等式的解为b<x<$\frac{1}{2}$,
综上若b=$\frac{1}{2}$,则不等式的解集为∅.
若b>$\frac{1}{2}$,则不等式的解集为($\frac{1}{2}$,b),
若b<$\frac{1}{2}$,则不等式的解集为(b,$\frac{1}{2}$).
点评 本题主要考查函数解析式的求解,利用函数奇偶性的定义是解决本题的关键.利用分类讨论的思想是解决含有参数的一元二次不等式的基本思想.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 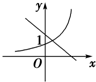 | B. |  | C. |  | D. |  |
| A. | 4 | B. | 2 | C. | 7 | D. | 5 |