题目内容
18.函数f(x)=ax与g(x)=-x+a的图象大致是( )| A. | 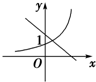 | B. |  | C. |  | D. |  |
分析 由直线g(x)=-x+a的斜率为-1可排除C,D;再对A,B选项判断即可.
解答 解:直线g(x)=-x+a的斜率为-1,
故排除C,D;
对于选项A,由函数f(x)=ax知a>1,由g(x)=-x+a知a>1;
对于选项B,由函数f(x)=ax知a>1,由g(x)=-x+a知0<a<1;
故选:A.
点评 本题考查了指数函数与一次函数的性质的判断与应用.

练习册系列答案
相关题目
8.已知f(x)是定义在R上的周期函数,最小正周期为T,则下列函数中恒为周期函数的是( )
| A. | f(x2+x) | B. | f(2x+x) | C. | f(sinx+x) | D. | f(f(x)+x) |
9.不等式m2+1≥2m中等号成立的条件是 ( )
| A. | m=1 | B. | m=±1 | C. | m=-1 | D. | m=0 |
6.下列数列是等比数列的是( )
| A. | 1,1,1,1,… | B. | …0,0,0,0, | C. | 0,12,14,18,… | D. | -1,-1,1,1 |
13.设bn=$\frac{{a}_{n}}{({a}_{n}+1)({a}_{n+1}+1)}$(其中an=2n-1),数列{bn}的前n项和为Tn,则T5=( )
| A. | $\frac{31}{33}$ | B. | $\frac{32}{33}$ | C. | $\frac{31}{66}$ | D. | $\frac{16}{33}$ |
3.“an=2n,n∈N*”是“数列{an}是等差数列”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |