题目内容
设函数
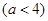
(1)若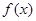 的最小值为3,求
的最小值为3,求 的值;
的值;
(2)求不等式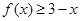 的解集.
的解集.
(1)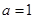 ;(2)
;(2)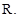
解析试题分析:本题考查绝对值不等式的解法和不等式恒成立问题,考查学生的分类讨论思想和转化能力以及计算能力.第一问,利用不等式的性质,得出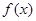 的最小值,列出等式,解出
的最小值,列出等式,解出 的值;第二问,解含参绝对值不等式,用零点分段法去掉绝对值,由于已知中有
的值;第二问,解含参绝对值不等式,用零点分段法去掉绝对值,由于已知中有 和4的大小,所以直接解不等式即可,最后综合上述所得不等式的解集.
和4的大小,所以直接解不等式即可,最后综合上述所得不等式的解集.
试题解析:⑴因为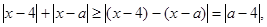
因为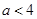 ,所以当且仅当
,所以当且仅当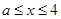 时等号成立,故
时等号成立,故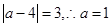 为所求. 4分
为所求. 4分
⑵不等式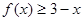 即不等式
即不等式
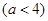 ,
,
①当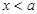 时,原不等式可化为
时,原不等式可化为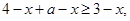
即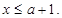
所以,当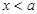 时,原不等式成立.
时,原不等式成立.
②当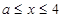 时,原不等式可化为
时,原不等式可化为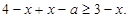
即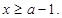 所以,当
所以,当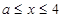 时,原不等式成立.
时,原不等式成立.
③当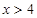 时,原不等式可化为
时,原不等式可化为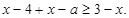
即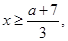 由于
由于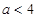 时
时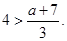
所以,当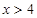 时,原不等式成立.
时,原不等式成立.
综合①②③可知: 不等式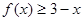 的解集为
的解集为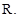 10分
10分
考点:1.不等式的性质;2.绝对值不等式的解法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
不等式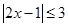 的解集为( )
的解集为( )
A.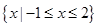 | B.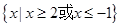 | C.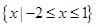 | D.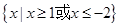 |
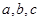 满足
满足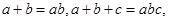 则
则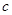 的取值范围是 .
的取值范围是 .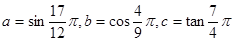 则从小到大的顺序为
则从小到大的顺序为 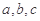 为三角形
为三角形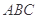 的三边,求证:
的三边,求证: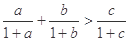
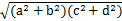 并指明等号何时成立.
并指明等号何时成立. 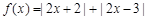 .
.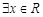 ,使得不等式
,使得不等式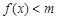 成立,求
成立,求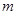 的取值范围;
的取值范围;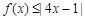 成立的
成立的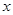 的取值范围.
的取值范围.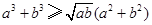 .
.