题目内容
已知函数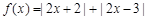 .
.
(Ⅰ)若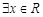 ,使得不等式
,使得不等式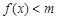 成立,求
成立,求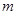 的取值范围;
的取值范围;
(Ⅱ)求使得等式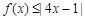 成立的
成立的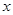 的取值范围.
的取值范围.
(Ⅰ)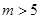 ;(Ⅱ)
;(Ⅱ)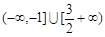 .
.
解析试题分析:(Ⅰ)根据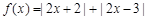 =
= 求出
求出 的最小值,从而求得得不等式
的最小值,从而求得得不等式 成立的
成立的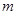 的取值范围.
的取值范围.
(Ⅱ)由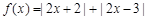
 =
=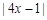 ,可知当且仅当
,可知当且仅当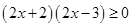 时有
时有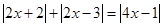 ,从而
,从而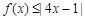 成立.解不等式
成立.解不等式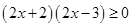 由此求得
由此求得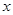 的取值范围.
的取值范围.
试题解析:(Ⅰ)由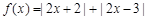 =
=
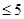 3分
3分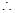 使得不等式
使得不等式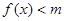 成立的
成立的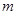 的取值范围是
的取值范围是 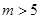 5分
5分
(Ⅱ)由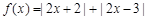
 =
=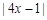 7分
7分
所以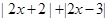
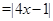 ,当且仅当
,当且仅当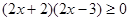 时取等 9分
时取等 9分
所以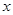 的取值范围是
的取值范围是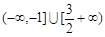 10分
10分
考点:1、绝对值不等式的性质;2、绝对值不等式的解法.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
不等式log2 ≥1的解集为( )
≥1的解集为( )
| A.(-∞,-1] | B.[-1,+∞) |
| C.[-1,0) | D.(-∞,-1]∪(0,+∞) |
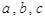 满足
满足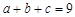 ,
,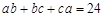 ,则
,则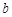 的取值范围是 .
的取值范围是 .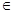 R
R
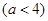
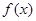 的最小值为3,求
的最小值为3,求 的值;
的值;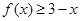 的解集.
的解集. ,
,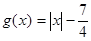 .
.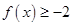 ;
;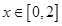 ,
,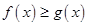 ,求
,求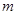 的取值范围.
的取值范围. (
(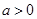 ).区间
).区间 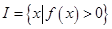 ,定义区间
,定义区间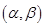 的长度为 b-a .
的长度为 b-a .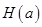 (用 a 表示);
(用 a 表示);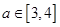 ,求
,求 。求证:
。求证: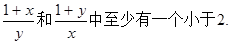
 ,则
,则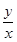 的最大值为 。
的最大值为 。