题目内容
【题目】已知椭圆 ![]() 抛物线
抛物线 ![]() 焦点均在
焦点均在 ![]() 轴上,
轴上, ![]() 的中心和
的中心和 ![]() 顶点均为原点
顶点均为原点 ![]() ,从每条曲线上各取两个点,将其坐标记录于表中,则
,从每条曲线上各取两个点,将其坐标记录于表中,则 ![]() 的左焦点到
的左焦点到 ![]() 的准线之间的距离为( )
的准线之间的距离为( )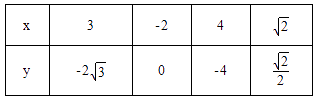
A.![]()
B.![]()
C.1
D.2
【答案】B
【解析】解:A、∵由表可知,抛物线 ![]() 焦点在
焦点在 ![]() 轴的正半轴,设抛物线
轴的正半轴,设抛物线 ![]() ,则有
,则有 ![]() , ∴将
, ∴将 ![]() 代入
代入 ![]() ,代入可得
,代入可得 ![]() ,即
,即 ![]() ∴抛物线
∴抛物线 ![]() 的标准方程为
的标准方程为 ![]() ,则焦点坐标为
,则焦点坐标为 ![]() ,准线方程为
,准线方程为 ![]() , 设椭圆
, 设椭圆 ![]() ,把点
,把点 ![]() 代入得,
代入得,  ,即
,即 ![]() ∴
∴ ![]() 的标准方程为
的标准方程为 ![]() ; ∵
; ∵ ![]() ∴左焦点
∴左焦点 ![]() ∴
∴ ![]() 的左焦点到 C2 的准线之间的距离
的左焦点到 C2 的准线之间的距离 ![]() 1,A不符合题意
1,A不符合题意![]()
B、 C1 的左焦点到 C2 的准线之间的距离 ![]() 1,B符合题意;
1,B符合题意;
C、 C1 的左焦点到 C2 的准线之间的距离 ![]() 1,C不符合题意;
1,C不符合题意;
D、 C1 的左焦点到 C2 的准线之间的距离 ![]() 1,D不符合题意。
1,D不符合题意。
故答案为:B.
过定点的椭圆方程可以设为:mX2+nY2=1;焦点在X轴上的椭圆方程可以设为:![]() +
+![]() =1(a>b>0);有共同焦点(
=1(a>b>0);有共同焦点(![]() ,0)的椭圆方程可以设为:
,0)的椭圆方程可以设为:![]() =1等。焦点在X轴的正半轴上的抛物线的标准方程可以设为:Y2=2px(p>0);焦点在X轴的负半轴上的抛物线的标准方程可以设为:Y2=-2px(p>0);焦点在X轴上的抛物线的标准方程可以设为:Y2=mX(m不等于0);焦点在Y轴上的抛物线的标准方程可以设为:X2=mY(m不等于0)等。
=1等。焦点在X轴的正半轴上的抛物线的标准方程可以设为:Y2=2px(p>0);焦点在X轴的负半轴上的抛物线的标准方程可以设为:Y2=-2px(p>0);焦点在X轴上的抛物线的标准方程可以设为:Y2=mX(m不等于0);焦点在Y轴上的抛物线的标准方程可以设为:X2=mY(m不等于0)等。

练习册系列答案
相关题目
【题目】宿州市某登山爱好者为了解山高y(百米)与气温x(℃)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表,由表中数据,得到线性回归方程为y=﹣2x+a,由此估计山高为72(百米)处的气温为( )
气温x(℃) | 18 | 13 | 10 | ﹣1 |
山高y(百米) | 24 | 34 | 38 | 64 |
A.﹣10
B.﹣8
C.﹣6
D.﹣4

