题目内容
设函数
(1)若函数 在
在 处取得极大值,求函数
处取得极大值,求函数 的单调递增区间;
的单调递增区间;
(2)若对任意实数 ,
, ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
【答案】
解:(1)
由条件知
所以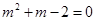
故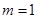 或
或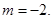 ……(2分)
……(2分)
当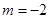 时,
时, 在
在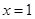 处取得极小值;
处取得极小值;
当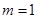 时,
时, 在
在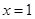 处取得极大值;
处取得极大值;
综上可知,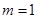 ……(4分)
……(4分)

由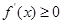 ,得
,得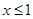 或
或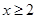 ;
;
故 的单调递增区间为
的单调递增区间为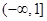 ,
, . ……(6分)
. ……(6分)

只需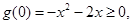 得
得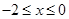 ,
,
即使原不等式恒成立的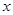 的取值范围是
的取值范围是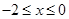 . ……(12分)
. ……(12分)
解法二:
由 ,及
,及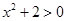 ,
,
可知对任意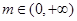 ,
, 恒成立.
恒成立.
故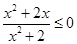 ,
……(10分)
,
……(10分)
又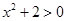 恒成立,
恒成立,
所以, ,
,
即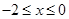 ,
,
故原不等式恒成立的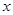 的取值范围是
的取值范围是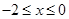 . ……(12分)
. ……(12分)
【解析】略

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
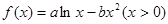
 在x=1处与直线
在x=1处与直线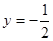 相切
相切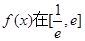 上的最大值.
上的最大值.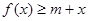 对所有的
对所有的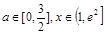 都成立,求实数m的取值范围.
都成立,求实数m的取值范围.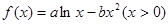
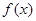 在x=1处与直线
在x=1处与直线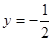 相切
相切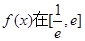 上的最大值.
上的最大值. 对所有的
对所有的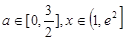 都成立,求实数m的取值范围.
都成立,求实数m的取值范围.