题目内容
已知函数 ,函数
,函数 .
.
⑴当 时,函数
时,函数 的图象与函数
的图象与函数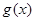 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值;
⑵当 时,试判断函数
时,试判断函数 的图象与函数
的图象与函数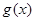 的图象的公共点的个数;
的图象的公共点的个数;
⑶函数 的图象能否恒在函数
的图象能否恒在函数 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
(1) 的最大值为
的最大值为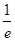 ,(2)
,(2)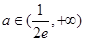 时,无公共点,
时,无公共点,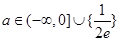 时,有一个公共点,
时,有一个公共点,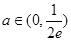 时,有两个公共点;(3)当
时,有两个公共点;(3)当 或
或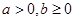 时函数
时函数 的图象恒在函数
的图象恒在函数 的图象的上方.
的图象的上方.
解析试题分析:(1)当 时,由图形可知一次函数
时,由图形可知一次函数 与对数函数
与对数函数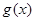 相切时,
相切时, 取最大值,可以用导数的几何意义完成;(2)要研究两函数的公共点个数,由函数
取最大值,可以用导数的几何意义完成;(2)要研究两函数的公共点个数,由函数 的定义域可知只需考虑
的定义域可知只需考虑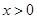 情况,当
情况,当 时,令
时,令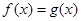 得
得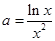 ,则原命题等价于研究直线
,则原命题等价于研究直线 与函数
与函数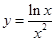 的图象的公共点的个数,因此利用导数研究函数
的图象的公共点的个数,因此利用导数研究函数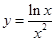 图象变化情况,易得结论;(3)把问题转化为:
图象变化情况,易得结论;(3)把问题转化为: 在
在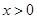 时恒成立问题,要注意对
时恒成立问题,要注意对 取值情况的讨论.
取值情况的讨论.
试题解析:⑴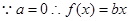 ,由一次函数与对数函数图象可知两图象相切时
,由一次函数与对数函数图象可知两图象相切时 取最大值,设切点横坐标为
取最大值,设切点横坐标为 ,
,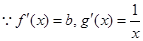 ,
,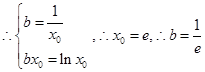 , 即实数
, 即实数 的最大值为
的最大值为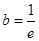 ,⑵
,⑵ ,即原题等价于直线
,即原题等价于直线 与函数
与函数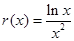 的图象的公共点的个数,
的图象的公共点的个数,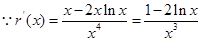 ,
,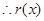 在
在 递增且
递增且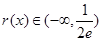 ,
,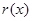 在
在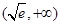 递减且
递减且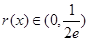 ,
,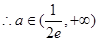 时,无公共点,
时,无公共点,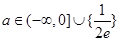 时,有一个公共点,
时,有一个公共点,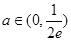 时,有两个公共点;⑶函数
时,有两个公共点;⑶函数 的图象恒在函数
的图象恒在函数 的上方;即
的上方;即 在
在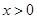 时恒成立,①
时恒成立,①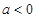 时
时 图象开口向下,即
图象开口向下,即 在
在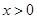 时不可能恒成立,②
时不可能恒成立,②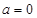 时
时 ,由⑴可得
,由⑴可得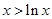 ,
, 时
时 恒成立,
恒成立,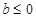 时
时 不成立,③
不成立,③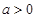 时,若
时,若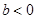 则
则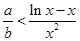 ,由⑵可得
,由⑵可得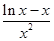 无最小值,故
无最小值,故 不可能恒成立,若
不可能恒成立,若 则
则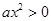 ,故
,故 恒成立,若
恒成立,若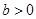 则
则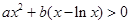 ,故
,故 恒成立,综上,
恒成立,综上, 或
或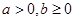 时,函数
时,函数 的图象恒在函数
的图象恒在函数 的图象的上方.
的图象的上方.
考点:导数的几何意义,用导数分析函数的单调性,最值,恒成立问题,渗透数形结合思想,分类讨论的数学思想

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
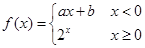 ,且
,且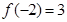 ,
,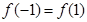 .
. 的解析式;
的解析式;
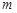 ,使得
,使得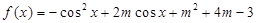 的最大值为
的最大值为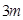 ,若存在,求出
,若存在,求出 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m, ;
; 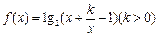 的值域为R,则实数k的取值范围是__________
的值域为R,则实数k的取值范围是__________ ”,“=”,“>”之一)
”,“=”,“>”之一)