题目内容
是否存在实数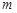 ,使得
,使得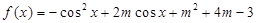 的最大值为
的最大值为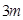 ,若存在,求出
,若存在,求出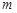 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
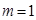 或
或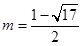
解析试题分析:由题设可假定存在,若能说明其成立则进而可求得其值,若能推出矛盾则说明其不存在.
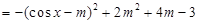 ,结合
,结合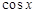 的取值范围,分类讨论
的取值范围,分类讨论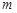 的取值范围,从而使得问题迎刃解决.分三种情况来讨论:ⅰ)当
的取值范围,从而使得问题迎刃解决.分三种情况来讨论:ⅰ)当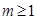 时;ⅱ)当
时;ⅱ)当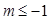 时;ⅲ)当
时;ⅲ)当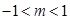 时.
时.
试题解析:
假设存在满足条件的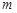 .
.
ⅰ)当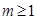 时,
时,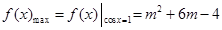
令 ,得
,得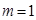 (
(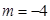 舍去)
舍去)
ⅱ)当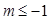 时,
时,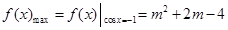
令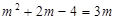 ,得
,得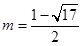 (
(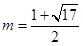 舍去)
舍去)
ⅲ)当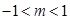 时,
时,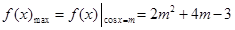
令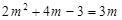 ,得
,得 (舍去)
(舍去)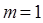 (舍去)
(舍去)
综上,存在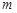 使得
使得 的最大值为
的最大值为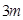 .
.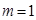 或
或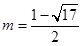
考点:函数参数存在性开放性问题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株为样本,统计结果如下:
| | 高茎 | 矮茎 | 合计 |
| 圆粒 | 11 | 19 | 30 |
| 皱粒 | 13 | 7 | 20 |
| 合计 | 24 | 26 | 50 |
(2)根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考):
| P(K2≥k) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
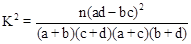 ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量. 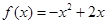 .
.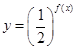 的最小值;
的最小值;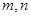 ,当
,当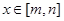 时,
时,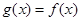 ,且
,且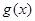 的值域为
的值域为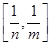 ?若存在,求出所有的
?若存在,求出所有的 ,函数
,函数 .
. 时,函数
时,函数 的图象与函数
的图象与函数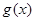 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值; 时,试判断函数
时,试判断函数 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.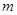 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式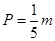 ,
, 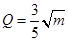 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资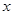 (单位:万元)
(单位:万元)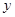 (单位:万元)关于
(单位:万元)关于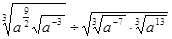 ;
;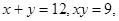 且
且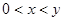 ,求
,求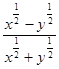 的值.
的值.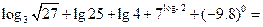
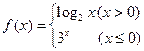 ,则
,则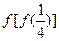 的值是___________
的值是___________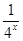 -
-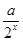 (a∈R).
(a∈R).