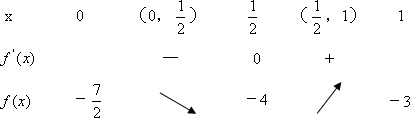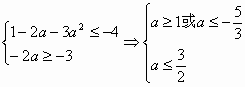Question

解答题：解答应写出文字说明，证明过程或演算步骤． (理科做)已知函数，x∈[0，1] (1) 求f(x)的单调区间和值域 (2) 设a≥1，函数g(x)＝x3－3a2x－2a，x∈[0，1]，若对于任意x1∈[0，1]，总存在x0∈[0，1]，使得g(x0)＝f(x1)成立，求a的取值范围．

Answer 1

答案：
解析：

(1)	令或　　　　　　　　　　　　　　2分 所以　　是减函数 　　是增函数　　　　　　　　　　　　　　　　4分 故时的值域为[－4，－3]　　　　　　　　　　　　　　　　6分
(2)	∵a≥1当时 ∴时g(x)↓ 时g(x)∈[g(1)，g(0)]＝[1－2a－3a2，－2a]　　　　　　　　8分 任给x1∈[0，1]　f(x1)∈[－4，－3] 存在x0∈[0，1]　使得g(x0)＝f(x1) 则：[1－2a－3a2，－2a]＝[－4，－3]　　　　　　　　　　　　　　　　10分 即 又a≥1故a的取值范围为[1，]　　　　　　　　　　　　　　　　　12分