题目内容
(本小题满分12分)
已知函数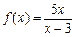 ,
,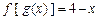 .(1)求
.(1)求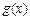 的解析式;(2) 求
的解析式;(2) 求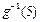 的值.
的值.
已知函数
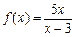 ,
,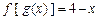 .(1)求
.(1)求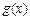 的解析式;(2) 求
的解析式;(2) 求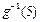 的值.
的值.(1) 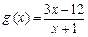 (2)
(2) 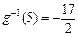
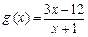 (2)
(2) 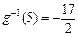
解:(1) ∵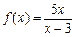 ,∴
,∴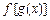
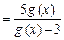
又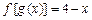 ,∴
,∴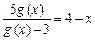 ,解得
,解得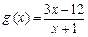 ;
;
(2) ∵ 反函数的自变量就是原函数的函数值
∴ 在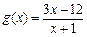 中有
中有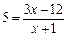 ,解得
,解得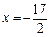 ,∴
,∴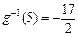 .
.
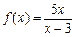 ,∴
,∴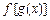
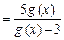
又
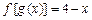 ,∴
,∴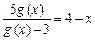 ,解得
,解得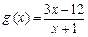 ;
;(2) ∵ 反函数的自变量就是原函数的函数值
∴ 在
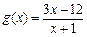 中有
中有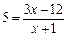 ,解得
,解得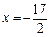 ,∴
,∴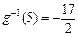 .
.
练习册系列答案
相关题目
题目内容
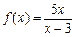 ,
,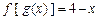 .(1)求
.(1)求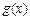 的解析式;(2) 求
的解析式;(2) 求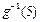 的值.
的值.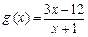 (2)
(2) 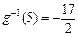
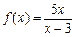 ,∴
,∴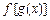
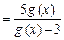
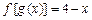 ,∴
,∴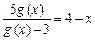 ,解得
,解得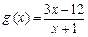 ;
;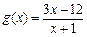 中有
中有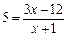 ,解得
,解得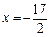 ,∴
,∴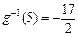 .
.