题目内容
19．已知抛物线y=$\frac{1}{2}$x2的焦点为F，准线为l，M在l上，线段MF与抛物线交于N点，若|MN|=$\sqrt{2}$|NF|，则|MF|=（ ）| A． | 2 | B． | 3 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
分析 作N到准线的垂线NH交准线于H点．根据抛物线的定义可知|NH|=|NF|，进而根据|NM|=$\sqrt{2}$|NH|，判断出∠NMH，进而推断出∠FMK，求得|MF|=$\sqrt{2}$|FK|，利用抛物线的方程求得|FK|，则|MF|可求．
解答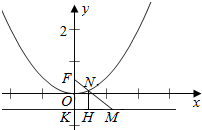 
解：作N到准线的垂线NH交准线于H点．
根据抛物线的定义可知|NH|=|NF|，
在△NHM中，|NM|=$\sqrt{2}$|NH|，则∠NMH=45°．
在△MFK中，∠FMK=45°，
所以|MF|=$\sqrt{2}$|FK|．而|FK|即为准焦距为1．
所以|MF|=$\sqrt{2}$．
故选：C．
点评 本题主要考查了抛物线的简单性质．考查了考生对抛物线定义的应用和数形结合思想的运用．
练习册系列答案
同步练习强化拓展系列答案
相关题目
10．下列命题中真命题的个数是（ ）
①?x∈R，x4＞x2；
②若p∧q是假命题，则p、q都是假命题；
③命题“?x∈R，x3+2x2+4≤0”的否命题为“?x0∈R，x03+2x02+4＞0”
①?x∈R，x4＞x2；
②若p∧q是假命题，则p、q都是假命题；
③命题“?x∈R，x3+2x2+4≤0”的否命题为“?x0∈R，x03+2x02+4＞0”
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
7．已知全集为R，集合A={x|（$\frac{1}{2}$）x≤1}，B={x|x≥2}，A∩（∁RB）=（ ）
| A． | [0，2） | B． | [0，2] | C． | （1，2） | D． | （1，2] |
14．若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的面积为abπ，则${∫}_{0}^{\frac{\sqrt{2}}{2}}$$\sqrt{1{-2x}^{2}}$dx=（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{8}$ | C． | $\frac{\sqrt{2}π}{4}$ | D． | $\frac{\sqrt{2}π}{8}$ |
如图1，在Rt△ABC中，∠ABC=90°，AB=BC=4，点E，F分别在线段AB，AC上，且EF∥BC，将△AEF沿EF折起到△PEF的位置，使得二面角P-EF-B的大小为60°（如图2）．