题目内容
【题目】以平面直角坐标系中的坐标原点为极点，
轴的正半抽为极轴，建立极坐标系，曲线
的极坐标方程是
，直线
的参数方程是
（
为参数）.
（1）求曲线的直角坐标方程；
（2）若直线与曲线交于
、
两点，且
，求直线的倾斜角
.
【答案】（1）
；（2）
或
.
【解析】
（1）在曲线
的极坐标的两边同时乘以
，再由
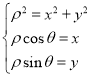，可将曲线的极坐标方程化为直角坐标方程；
（2）将直线
的参数方程代入曲线的直角坐标方程，得到关于
的一元二次方程，并列出韦达定理，借助弦长公式即可计算出
的值.
（1）在曲线的极坐标的两边同时乘以，得
，
所以，曲线的直角坐标方程为
，即；
（2）设点
、
在直线上对应的参数分别为
、
，
将直线的参数方程代入曲线的直角坐标方程，得
，
即
，
，
由韦达定理得
，
，
，得
，
，因此，
或.
阅读快车系列答案
【题目】某公司为确定下一年度投入某种产品的宜传费，需了解年宣传费对年销售量（单位：t）的影响.该公司对近5年的年宣传费和年销售量数据进行了研究，发现年宣传费x（万元）和年销售量y（单位：t）具有线性相关关系，并对数据作了初步处理，得到下面的一些统计量的值.
x（万元） | 2 | 4 | 5 | 3 | 6 |
y（单位：t） | 2.5 | 4 | 4.5 | 3 | 6 |
（1）根据表中数据建立年销售量y关于年宣传费x的回归方程.
（2）已知这种产品的年利润
（万元）与x，y的关系为
根据（1）中的结果回答下列问题：
①当年宣传费为10万元时，预测该产品的年销售量及年利润；
②估计该产品的年利润与年宣传费的比值的最大值.
附：回归方程
中的斜率和截距的最小二乘估计公式分别为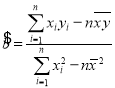
.
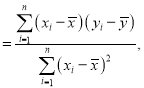
参考数据：
.
【题目】某省数学学会为选拔一批学生代表该省参加全国高中数学联赛，在省内组织了一次预选赛，该省各校学生均可报名参加.现从所有参赛学生中随机抽取
人的成绩进行统计，发现这名学生中本次预选赛成绩优秀的男、女生人数之比为
，成绩一般的男、女生人数之比为
.已知从这名学生中随机抽取一名学生，抽到男生的概率是
（1）请将下表补充完整，并判断是否有
的把握认为在本次预选赛中学生的成绩优秀与性别有关？
成绩优秀 | 成绩一般 | 总计 | |
男生 | |||
女生 | |||
总计 |
|
（2）以样本估计总体，视样本频率为相应事件发生的概率，从所有本次预选赛成绩优秀的学生中随机抽取
人代表该省参加全国联赛，记抽到的女生人数为
，求随机变量的分布列及数学期望.
参考公式：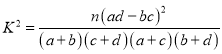
，其中
；
临界值表供参考：
|
|
|
|
|
|
|
|
|
|
|
|
