题目内容
已知点C为y2=2px(p>0)的准线与x轴的交点,点F为焦点,点A、B为抛物线上两个点,若
+
+2
=
则向量
与
的夹角为
.
| FA |
| FB |
| FC |
| 0, |
| FA |
| FB |
| 2π |
| 3 |
| 2π |
| 3 |
分析:设出点A,B的坐标,利用点A、B是抛物线上的两个点,
+
+2
=
可求
,
的坐标,再利用向量的夹角公式,即可得出结论.
| FA |
| FB |
| FC |
| 0, |
| FA |
| FB |
解答:解:设A(x1,y1),B(x2,y2),抛物线y2=2px(p>0)的准线与x轴的交点C(-
,0),焦点F(
,0)
∵
+
+2
=
∴(x1-
,y1)+(x2-
,y2)+(-2p,0)=(0,0)
∴x1+x2=3p,y1+y2=0
∵y12=2px1,y22=2px2,
∴y12+y22=2p(x1+x2)
∴y12=y22=3p2,x1=x2=
p
∴
=(p,
p),
=(p,-
p)
设向量
,
的夹角为α,则cosα=
=
=-
∵α∈[0,π]
∴α=
故答案为:
.
| p |
| 2 |
| p |
| 2 |
∵
| FA |
| FB |
| FC |
| 0 |
∴(x1-
| p |
| 2 |
| p |
| 2 |
∴x1+x2=3p,y1+y2=0
∵y12=2px1,y22=2px2,
∴y12+y22=2p(x1+x2)
∴y12=y22=3p2,x1=x2=
| 3 |
| 2 |
∴
| FA |
| 3 |
| FB |
| 3 |
设向量
| FA |
| FB |
| ||||
|
|
| p2-3p 2 |
| 4p2 |
| 1 |
| 2 |
∵α∈[0,π]
∴α=
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题考查抛物线的简单性质,向量知识的运用,考查向量的夹角公式,解题的关键是确定向量的坐标.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知点M是抛物线y2=2px(p>0)位于第一象限部分上的一点,且点M与焦点F的距离|MF|=2p,则点M的坐标为( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
 ,
, p)
p) ,
, p)
p) ,
, p)
p)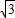 p,
p, )
)