题目内容
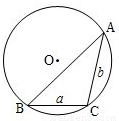
通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.(1)如图所示,在以O为圆心,半径为2的⊙O中,BC和BA是⊙O的弦,其中BC=2,∠ABC=45°,求弦AB的长;
(2)在△ABC中,若∠C是钝角,求证:a2+b2<4R2;
(3)给定三个正实数a、b、R,其中b≤a,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的△ABC不存在,存在一个或两个(全等的三角形算作同一个)?在△ABC存在的情况下,用a、b、R表示c.
【答案】分析:(1)由正弦定理知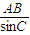 =
=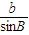 =
=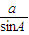 =2R,根据题目中所给的条件,不难得出弦AB的长;
=2R,根据题目中所给的条件,不难得出弦AB的长;
(2)若∠C是钝角,故其余弦值小于0,由余弦定理得到a2+b2<c2<(2R)2,即可证得结果;
(3)根据图形进行分类讨论判断三角形的形状与两边a,b的关系,以及与直径的大小的比较,分成三类讨论即可.
解答:解:(1)在△ABC中,BC=2,∠ABC=45°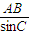 =
=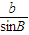 =
=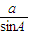 =2R⇒b=2
=2R⇒b=2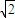
sinA= ∵A为锐角∴A=30°,B=45°
∵A为锐角∴A=30°,B=45°
∴C=75°∴AB=2Rsin75°=4sin75°=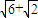 ;
;
(2)∠C为钝角,∴cosC<0,且cosC≠1
cosC=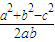 <0∴a2+b2<c2<(2R)2
<0∴a2+b2<c2<(2R)2
即a2+b2<4R2(8分)
(3)a>2R或a=b=2R时,△ABC不存在
当 时,A=90,△ABC存在且只有一个
时,A=90,△ABC存在且只有一个
∴c=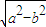
当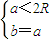 时,∠A=∠B且都是锐角sinA=sinB=
时,∠A=∠B且都是锐角sinA=sinB=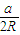 时,△ABC存在且只有一个
时,△ABC存在且只有一个
∴c=2RsinC=2Rsin2AC=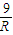
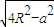
当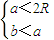 时,∠B总是锐角,∠A可以是钝角,可是锐角
时,∠B总是锐角,∠A可以是钝角,可是锐角
∴△ABC存在两个
∠A<90°时,
c=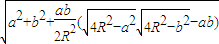
∠A>90°时,
c=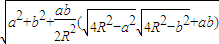
点评:本题考查三角形中的几何计算,综合考查了三角形形状的判断,解三角形,三角形的外接圆等知识,综合性很强,尤其是第三问需要根据a,b两边以及直径的大小比较确定三角形的形状.再在这种情况下求第三边的表达式,本解法主观性较强.难度较大.
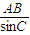 =
=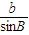 =
=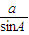 =2R,根据题目中所给的条件,不难得出弦AB的长;
=2R,根据题目中所给的条件,不难得出弦AB的长;(2)若∠C是钝角,故其余弦值小于0,由余弦定理得到a2+b2<c2<(2R)2,即可证得结果;
(3)根据图形进行分类讨论判断三角形的形状与两边a,b的关系,以及与直径的大小的比较,分成三类讨论即可.
解答:解:(1)在△ABC中,BC=2,∠ABC=45°
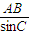 =
=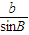 =
=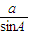 =2R⇒b=2
=2R⇒b=2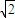
sinA=
 ∵A为锐角∴A=30°,B=45°
∵A为锐角∴A=30°,B=45°∴C=75°∴AB=2Rsin75°=4sin75°=
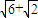 ;
;(2)∠C为钝角,∴cosC<0,且cosC≠1
cosC=
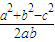 <0∴a2+b2<c2<(2R)2
<0∴a2+b2<c2<(2R)2即a2+b2<4R2(8分)
(3)a>2R或a=b=2R时,△ABC不存在
当
 时,A=90,△ABC存在且只有一个
时,A=90,△ABC存在且只有一个∴c=
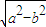
当
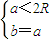 时,∠A=∠B且都是锐角sinA=sinB=
时,∠A=∠B且都是锐角sinA=sinB=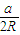 时,△ABC存在且只有一个
时,△ABC存在且只有一个∴c=2RsinC=2Rsin2AC=
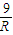
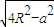
当
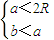 时,∠B总是锐角,∠A可以是钝角,可是锐角
时,∠B总是锐角,∠A可以是钝角,可是锐角∴△ABC存在两个
∠A<90°时,
c=
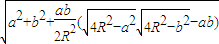
∠A>90°时,
c=
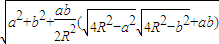
点评:本题考查三角形中的几何计算,综合考查了三角形形状的判断,解三角形,三角形的外接圆等知识,综合性很强,尤其是第三问需要根据a,b两边以及直径的大小比较确定三角形的形状.再在这种情况下求第三边的表达式,本解法主观性较强.难度较大.

练习册系列答案
相关题目
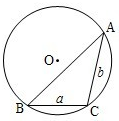 通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.
通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径. 通常用a、b、c分别表示△ABC的三个内角A,B,C所对边的边长,R表示△ABC的外接圆半径.
通常用a、b、c分别表示△ABC的三个内角A,B,C所对边的边长,R表示△ABC的外接圆半径. ;
;

