��Ŀ����
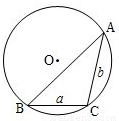
 ͨ����a��b��c��ʾ��ABC�������ڽǡ�A����B����C���Աߵı߳���R��ʾ��ABC���Բ�뾶��
ͨ����a��b��c��ʾ��ABC�������ڽǡ�A����B����C���Աߵı߳���R��ʾ��ABC���Բ�뾶����1����ͼ��ʾ������OΪԲ�ģ��뾶Ϊ2�ġ�O�У�BC��BA�ǡ�O���ң�����BC=2����ABC=45�㣬����AB�ij���
��2���ڡ�ABC�У�����C�Ƕ۽ǣ���֤��a2+b2��4R2��
��3������������ʵ��a��b��R������b��a���ʣ�a��b��R���������Ĺ�ϵʱ����a��bΪ�߳���RΪ���Բ�뾶�ġ�ABC�����ڣ�����һ����������ȫ�ȵ�����������ͬһ�������ڡ�ABC���ڵ�����£���a��b��R��ʾc��
��������1�������Ҷ���֪
=
=
=2R��������Ŀ�����������������ѵó���AB�ij���
��2������C�Ƕ۽ǣ���������ֵС��0�������Ҷ����õ�a2+b2��c2����2R��2������֤�ý����
��3������ͼ�ν��з��������ж������ε���״������a��b�Ĺ�ϵ���Լ���ֱ���Ĵ�С�ıȽϣ��ֳ��������ۼ��ɣ�
| AB |
| sinC |
| b |
| sinB |
| a |
| sinA |
��2������C�Ƕ۽ǣ���������ֵС��0�������Ҷ����õ�a2+b2��c2����2R��2������֤�ý����
��3������ͼ�ν��з��������ж������ε���״������a��b�Ĺ�ϵ���Լ���ֱ���Ĵ�С�ıȽϣ��ֳ��������ۼ��ɣ�
����⣺��1���ڡ�ABC�У�BC=2����ABC=45��
=
=
=2R?b=2
sinA=
��AΪ��ǡ�A=30�㣬B=45��
��C=75���AB=2Rsin75��=4sin75��=
+
��
��2����CΪ�۽ǣ���cosC��0����cosC��1
cosC=
��0��a2+b2��c2����2R��2
��a2+b2��4R2��8�֣�
��3��a��2R��a=b=2Rʱ����ABC������
��
ʱ��A=90����ABC������ֻ��һ��
��c=
��
ʱ����A=��B�Ҷ������sinA=sinB=
ʱ����ABC������ֻ��һ��
��c=2RsinC=2Rsin2AC=
��
ʱ����B������ǣ���A�����Ƕ۽ǣ��������
���ABC��������
��A��90��ʱ��
c=
��A��90��ʱ��
c=
| AB |
| sinC |
| b |
| sinB |
| a |
| sinA |
| 2 |
sinA=
| 1 |
| 2 |
��C=75���AB=2Rsin75��=4sin75��=
| 6 |
| 2 |
��2����CΪ�۽ǣ���cosC��0����cosC��1
cosC=
| a2+b2-c2 |
| 2ab |
��a2+b2��4R2��8�֣�
��3��a��2R��a=b=2Rʱ����ABC������
��
|
��c=
| a2-b2 |
��
|
| a |
| 2R |
��c=2RsinC=2Rsin2AC=
| 9 |
| R |
| 4R2-a2 |
��
|
���ABC��������
��A��90��ʱ��
c=
a2+b2+
|
��A��90��ʱ��
c=
a2+b2+
|
���������⿼���������еļ��μ��㣬�ۺϿ�������������״���жϣ��������Σ������ε����Բ��֪ʶ���ۺ��Ժ�ǿ�������ǵ�������Ҫ����a��b�����Լ�ֱ���Ĵ�С�Ƚ�ȷ�������ε���״���������������������ߵı���ʽ�����ⷨ�����Խ�ǿ���ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
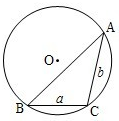
 ͨ����a��b��c�ֱ��ʾ��ABC�������ڽ�A��B��C���Աߵı߳���R��ʾ��ABC�����Բ�뾶��
ͨ����a��b��c�ֱ��ʾ��ABC�������ڽ�A��B��C���Աߵı߳���R��ʾ��ABC�����Բ�뾶�� ��
��