Question

通常用a、b、c分别表示△ABC的三个内角A，B，C所对边的边长，R表示△ABC的外接圆半径．
（1）如图，在以O为圆心、直径为8的⊙O中，BC和BA是⊙O的弦，其中BC=4，∠ABC=45°，求弦AB的长；
（2）在△ABC中，若∠C是钝角，求证：a²+b²＜4R²．

Answer 1

分析：（1）利用正弦定理求出A，通过两角和的正弦函数，求出C，然后求弦AB的长；
（2）法一；利用余弦定理推出a²+b²＜c²，利用正弦定理推出a²+b²＜4R²．
法二：利用正弦定理求出A，通过余弦定理求出C，然后证明a²+b²＜4R²．

解答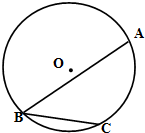：解 （1）△ABC的外接圆半径为4，在△ABC中，
sinA=

BC

2R

=

4

8

=

1

2

，∴A=30°（A=150°不合题意）（3分）
∴sinC=sin[π-（A+B）]=sin（A+B）=sinAcosB+cosAsinB）=

1

2

×

2

2

+

3

2

×

2

2

=

6 + 2

4

（5分）
∴AB=2RsinC=8×

6 + 2

4

=2(

6

+

2)

（6分）
（2）证明：法1：由余弦定理得cosC=

a2+b2-c2

2ab

，∵C为钝角∴cosC＜0，∴a²+b²＜c²（9分）
又由正弦定理得c=2RsinC＜2R，∴c²＜4R²，∴a²+b²＜4R²（12分）
法2：∵sinA=

a

2R

，sinB=

b

2R

，由于∠C是钝角，∠A、∠B都是锐角，得cosA=

1

2R

4R2-a2

，cosB=

1

2R

4R2-b2

，（8分）
cosC=-cos（A+B）=-cosAcosB+sinAsinB=

1

4R2

(ab-

4R2-a2

4R2-b2

)＜0，（10分）
∴a²b²＜（4R²-a²）（4R²-b²），∴16R⁴-4R²（a²+b²）＞0，即a²+b²＜4R²．（ 12分）

点评：本题考查正弦定理与余弦定理的应用，三角形的解法，考查计算能力．