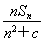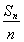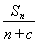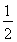Question

已知在等差数列{an}中，a1＝31，Sn是它的前n项和，S10＝S22.

(1)求Sn；

(2)这个数列的前多少项的和最大，并求出这个最大值．

 

Answer 1

（1）32n－n2（2）n＝16时，Sn有最大值256.

【解析】(1)∵S10＝a1＋a2＋…＋a10，S22＝a1＋a2＋…＋a22，S10＝S22，∴a11＋a12＋…＋a22＝0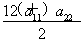，＝0，即a11＋a22＝2a1＋31d＝0.又a1＝31，∴d＝－2，

∴Sn＝na1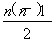＋d＝31n－n(n－1)＝32n－n2.

(2)解法1：由(1)知Sn＝32n－n2，∴当n＝16时，Sn有最大值，Sn的最大值是256.

解法2：由Sn＝32n－n2＝n(32－n)，欲使Sn有最大值，应有1<n<32，从而Sn≤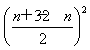＝256，当且仅当n＝32－n，即n＝16时，Sn有最大值256.