题目内容
3.已知函数f(x)=-x3+x2+b,若f(x)在x∈[-$\frac{1}{2}$,1]上的最大值为1,则实数b=$\frac{5}{8}$.分析 求出原函数的导函数,得到函数在[-$\frac{1}{2}$,1]上的单调区间,求出函数的最值,由最大值为1求出b的值.
解答 解:∵f(x)=-x3+x2+b,∴f′(x)=-3x2+2x,由f′(x)=0,得${x}_{1}=0,{x}_{2}=\frac{2}{3}$,
∴当0<x<$\frac{2}{3}$时,f′(x)>0;
当x<0或>$\frac{2}{3}$时,f′(x)<0.
∴f(x)在x∈[-$\frac{1}{2}$,0]上为减函数,在[$\frac{2}{3},1$]上为减函数,在[0,$\frac{2}{3}$]上为增函数.
而f(-$\frac{1}{2}$)=$\frac{1}{8}+\frac{1}{4}+b=\frac{3}{8}+b$,f($\frac{2}{3}$)=$-\frac{8}{27}+\frac{4}{9}+b=\frac{4}{27}+b$,且$\frac{3}{8}+b>\frac{4}{27}+b$,
∴$\frac{3}{8}+b=1$,则b=$\frac{5}{8}$.
故答案为:$\frac{5}{8}$.
点评 本题考查了利用导数求闭区间上函数的最值,求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.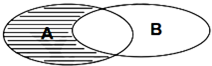 设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )
设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )
 设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )
设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )| A. | {x|0≤x<3} | B. | {x|0≤x<1} | C. | {x|-3<x<0} | D. | {x|0<x<1} |
8.若a+b=m${\;}^{\frac{1}{3}}$,ab=$\frac{1}{6}$m${\;}^{\frac{2}{3}}$(a>b),则a3+b3的值为( )
| A. | 0 | B. | $\frac{m}{2}$ | C. | -$\frac{m}{2}$ | D. | $\frac{3}{2}$m |