题目内容
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点. 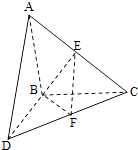
(1)求证:EF⊥BC;
(2)求二面角E﹣BF﹣C的正弦值.
【答案】
(1)证明:由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,
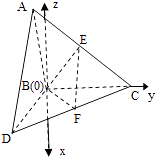
易得B(0,0,0),A(0,﹣1, ![]() ),D(
),D( ![]() ,﹣1,0),C(0,2,0),因而E(0,
,﹣1,0),C(0,2,0),因而E(0, ![]() ,
, ![]() ),F(
),F( ![]() ,
, ![]() ,0),所以
,0),所以 ![]() =(
=( ![]() ,0,﹣
,0,﹣ ![]() ),
), ![]() =(0,2,0),因此
=(0,2,0),因此 ![]()
![]() =0,所以EF⊥BC.
=0,所以EF⊥BC.
(2)解:在图中,设平面BFC的一个法向量 ![]() =(0,0,1),平面BEF的法向量
=(0,0,1),平面BEF的法向量 ![]() =(x,y,z),又
=(x,y,z),又 ![]() =(
=( ![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,
, ![]() ),
),
由 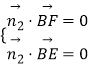 得其中一个
得其中一个 ![]() =(1,﹣
=(1,﹣ ![]() ,1),
,1),
设二面角E﹣BF﹣C的大小为θ,由题意知θ为锐角,则
cosθ=|cos< ![]() ,
, ![]() >|=|
>|=| 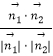 |=
|= ![]() ,
,
因此sinθ= ![]() =
= ![]() ,即所求二面角正弦值为
,即所求二面角正弦值为 ![]() .
.
【解析】(1)以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,得到E、F、B、C点的坐标,易求得此 ![]()
![]() =0,所以EF⊥BC;(2)设平面BFC的一个法向量
=0,所以EF⊥BC;(2)设平面BFC的一个法向量 ![]() =(0,0,1),平面BEF的法向量
=(0,0,1),平面BEF的法向量 ![]() =(x,y,z),依题意,可求得一个
=(x,y,z),依题意,可求得一个 ![]() =(1,﹣
=(1,﹣ ![]() ,1),设二面角E﹣BF﹣C的大小为θ,可求得sinθ的值.
,1),设二面角E﹣BF﹣C的大小为θ,可求得sinθ的值.

练习册系列答案
相关题目
