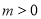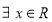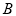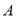题目内容
如图,在四棱锥 中,
中, 底面
底面 ,底面
,底面 是平行四边形,
是平行四边形, ,
, 是
是 的中点。
的中点。

(1)求证: ;
;
(2)求证: ;
;
(3)若 ,求二面角
,求二面角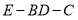 的余弦值.
的余弦值.
(1)详见解析;(2)详见解析;(3)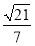
【解析】
试题分析:(1)连接AC交BD于F,连接EF,由ABCD是平行四边形,知F为AC的中点,由E为SC的中点,知SA∥EF,由此能够证明SA∥平面BDE.
(2)由AB=2,AD=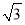 ,∠BAD=30°,利用余弦定理得BD=1,由AD2+BD2=AB2,知AD⊥BD.由此能够证明AD⊥SB.
,∠BAD=30°,利用余弦定理得BD=1,由AD2+BD2=AB2,知AD⊥BD.由此能够证明AD⊥SB.
(3)以DA为x轴,以DB为y轴,以DS为z轴,建立空间直角坐标系,利用向量法能够求出二面角E-BD-C的余弦值.
试题解析:(1)证明:连接AC交BD于F,连结EF,由ABCD是平行四边形,知F为AC的中点,又E为SC的中点,所以SA∥EF,∵SA?平面BDE,EF?平面BDE,
∴SA∥平面BDE. 4分
(2)由AB=2,AD=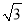 ,∠BAD=30?,由余弦定理得
,∠BAD=30?,由余弦定理得
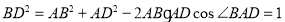
∵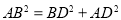 ∴AD⊥BD.
∴AD⊥BD.
∵SD⊥平面ABCD,AD?平面ABCD,
∴AD⊥SD,
∴AD⊥平面SBD,又SB?平面SBD,
∴AD⊥SB. 8分
(3)取CD的中点G,连结EG,FG,

则EG⊥平面BCD,且EG=1,FG∥BC,且FG=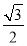
∵AD⊥BD, AD∥BC,∴FG⊥BD,又∵EG⊥BD ∴BD⊥平面EFG,
∴BD⊥EF,故∠EFG是二面角E—BD—C的平面角
在Rt△EFG中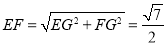
∴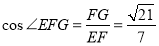 . 12分
. 12分
考点:(1)空间线面的位置关系;(2)二面角的求法;(3)向量在立体几何中的应用.

练习册系列答案
相关题目