题目内容
设| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
分析：根据|
|=|
|=|
+
|=2，得到由两个向量为邻边组成的四边形是菱形，且一条对角线等于边长，得到特殊的关系，最后利用余弦定理求出另一对角线长即可求出所求．
| a |
| b |
| a |
| b |
解答：解：∵|
|=|
|=|
+
|=2
由向量加法平行四边形法则得到由两个向量为邻边组成的四边形是菱形，
菱形的一条对角线同边相等，
，
的夹角为120°
而|
|=|
|=|
+
|=2，利用余弦定理得到另一条对角线长为2
∴|
-
|=2
故答案为：2
．
| a |
| b |
| a |
| b |
由向量加法平行四边形法则得到由两个向量为邻边组成的四边形是菱形，
菱形的一条对角线同边相等，
| a |
| b |
而|
| a |
| b |
| a |
| b |
| 3 |
∴|
| a |
| b |
| 3 |
故答案为：2
| 3 |
点评：大小和方向是向量的两个要素，分别是向量的代数特征和几何特征，借助于向量可以实现某些代数问题与几何问题的相互转化．
练习册系列答案
全能测控期末小状元系列答案
相关题目
，
是两个非零向量，则“向量
，
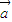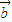是两个非零向量，则“向量
，
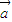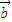的夹角为锐角”是“函数f（x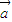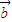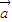）=（x
+
）•（
-x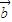
）的图象是一条开口向下的抛物线”的（ ）