题目内容
13.已知向量$\overrightarrow a$ 与$\overrightarrow b$ 的夹角为120°,且$|\overrightarrow a|=2$,$|\overrightarrow b|=1$,则$|\overrightarrow a+2\overrightarrow b|$=2.分析 利用数量积运算性质即可得出.
解答 解:∵向量$\overrightarrow a$ 与$\overrightarrow b$ 的夹角为120°,且$|\overrightarrow a|=2$,$|\overrightarrow b|=1$,
∴$\overrightarrow{a}•\overrightarrow{b}$=2×1×cos120°=-1.
则$|\overrightarrow a+2\overrightarrow b|$=$\sqrt{{\overrightarrow{a}}^{2}+4{\overrightarrow{b}}^{2}+4\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{4+4-4×(-1)}$=2.
故答案为:2.
点评 本题查克拉数量积运算性质,属于基础题.

练习册系列答案
相关题目
3.已知角α的终边经过点P(0,3),则α是( )
| A. | 第一象限角 | B. | 终边在x轴的非负半轴上的角 | ||
| C. | 第四象限角 | D. | 终边在y轴的非负半轴上的角 |
4.若方程($\frac{1}{4}$)x+($\frac{1}{2}$x-1+a=0)有正数解,则实数a的取值范围是( )
| A. | 0<a<1 | B. | -3<a<0 | C. | -2<a<0 | D. | -1<a<0 |
1.为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息,设定原信息为a0a1a2,ai∈{0,1}(i=0,1,2),传输信息为h0a0a1a2h1,其中h0=a0⊕a1,h1=h0⊕a2.⊕运算规则为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( )
| A. | 10111 | B. | 01100 | C. | 11010 | D. | 00011 |
5.已知等比数列{an}前n项和为Sn,且a2015=3S2014+2015,a2014=3S2013+2015,则公比q等于( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 4 | D. | $\frac{1}{4}$ |
2.在3x+2y<6表示的平面区域内的一个点是( )
| A. | (3,0) | B. | (1,3) | C. | (0,3) | D. | (0,0) |
3.设全集U=R,A={x||x|<2},B={x|y=$\sqrt{x-1}$},则图中阴影部分所表示的集合( )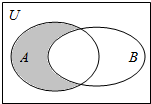

| A. | (-2,+∞) | B. | (1,2] | C. | (-2,1) | D. | (-2,1] |