题目内容
12、从A、B、C、D、E、F这6名运动员中选派4人参加4×100接力赛，参赛者每人只跑一棒，其中第一棒只能从A、B中选一人，第四棒只能从C、D、E中选一人，则不同的选派方案共有
72
种．分析：由题意知本题是一个分步计数问题，先排限制条件多的元素，第一棒只能从A、B中选一人，第四棒只能从C、D、E中选一人，余下的两个位置从四个元素中选两个排列，根据分步计数原理得到结果．
解答：解：由题意知本题是一个分步计数问题，
∵第一棒只能从A、B中选一人，第四棒只能从C、D、E中选一人
∴第一棒有C21种结果，
第四棒有C31种结果，
余下的两个位置从四个元素中选两个排列共有A42种结果，
∴不同的选派方法C21C31A42=72．
故答案为：72．
∵第一棒只能从A、B中选一人，第四棒只能从C、D、E中选一人
∴第一棒有C21种结果，
第四棒有C31种结果，
余下的两个位置从四个元素中选两个排列共有A42种结果，
∴不同的选派方法C21C31A42=72．
故答案为：72．
点评：排列与组合问题要区分开，若题目要求元素的顺序则是排列问题，排列问题要做到不重不漏，有些题目带有一定的约束条件，解题时要先考虑有限制条件的元素．
练习册系列答案
相关题目
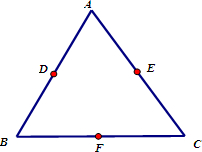（2012•江苏一模）如图，已知面积为1的正三角形ABC三边的中点分别为D、E、F，从A，B，C，D，E，F六个点中任取三个不同的点，所构成的三角形的面积为X（三点共线时，规定X=0）