题目内容
10、从A，B，C，D，E，F这6种不同的花朵中选出4种，插入4只不同的花瓶中展出，如果第1只花瓶内不能插入C，那么不同的插法种数为
480
．分析：本题是一个分类计数问题，当选出的四朵花不含有C时，有A54种结果，当选出的四朵花包含C时，先选出3朵花和C一起排列，C有三种结果，余下的三朵花在三个位置全排列．
解答：解：由题意知本题是一个分类计数问题，
当选出的四朵花不含有C时，有A54=120种结果，
当选出的四朵花包含C时，先选出3朵花和C一起排列，C有三种结果，
余下的三朵花在三个位置全排列有C63C31A33=360
根据分类计数原理得到共有120+360=480
故答案为：480
当选出的四朵花不含有C时，有A54=120种结果，
当选出的四朵花包含C时，先选出3朵花和C一起排列，C有三种结果，
余下的三朵花在三个位置全排列有C63C31A33=360
根据分类计数原理得到共有120+360=480
故答案为：480
点评：本题考查计数原理的应用，本题解题的关键是看出对于选C和不选C结果不同，因此考虑分类来解，注意做到不重不漏．
练习册系列答案
相关题目
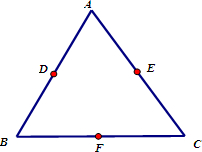（2012•江苏一模）如图，已知面积为1的正三角形ABC三边的中点分别为D、E、F，从A，B，C，D，E，F六个点中任取三个不同的点，所构成的三角形的面积为X（三点共线时，规定X=0）