题目内容
【题目】在矩形![]() 中,
中,![]() ,点
,点![]() 为线段
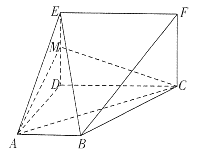
为线段![]() 中点,如图3所示,将
中点,如图3所示,将![]() 沿着
沿着![]() 翻折至
翻折至![]() (点
(点![]() 不在平面
不在平面![]() 内),记线段
内),记线段![]() 中点为
中点为![]() ,若三棱锥
,若三棱锥![]() 体积的最大值为
体积的最大值为![]() ,则线段
,则线段![]() 长度的最大值为___.
长度的最大值为___.
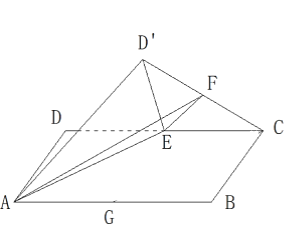
【答案】4
【解析】
取AB得中点G,连接CG,易得![]() ,
,![]() ,得点
,得点![]() 到平面
到平面![]() 的距离即为直线
的距离即为直线![]() 到平面
到平面![]() 的距离,可求出直线
的距离,可求出直线![]() 到面
到面![]() 的最大值, ,设
的最大值, ,设![]() ,可得F点到平面
,可得F点到平面![]() 的距离为
的距离为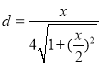 ,代入三棱锥体积的计算公式可得答案.
,代入三棱锥体积的计算公式可得答案.
解:由题意得:设F点到平面![]() 的距离为d,
的距离为d,
由线段![]() 中点为
中点为![]() ,可得点
,可得点![]() 到平面
到平面![]() 的距离为2d,
的距离为2d,
如图取AB得中点G,连接CG,易得![]() ,
,![]() ,得点
,得点![]() 到平面
到平面![]() 的距离即为直线
的距离即为直线![]() 到平面
到平面![]() 的距离,
的距离,
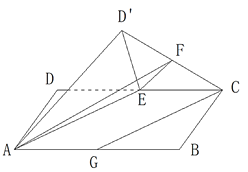
易得直线![]() 到平面
到平面![]() 的距离小于等于直线
的距离小于等于直线![]() 到直线
到直线![]() 的距离,
的距离,
再![]() 中,设
中,设![]() ,直线
,直线![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
可得![]() ,可得
,可得![]() ,
,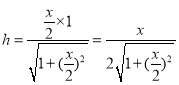 ,
,
由三棱锥![]() 体积的最大值为
体积的最大值为![]() ,可得
,可得![]() ,
,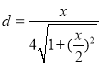 ,
,
可得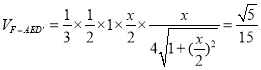 ,可得
,可得![]() ,
,
故答案为:4.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
【题目】某校夏令营有3名男同学![]() 和3名女同学
和3名女同学![]() ,其年级情况如下表:
,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
用表中字母列举出所有可能的结果
设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件![]() 发生的概率.
发生的概率.