题目内容
已知数列{an}满足:Sn=1-an(n∈N*),其中Sn为数列{an}的前n项和.
(1)求{an}的通项公式;
(2)若数列{bn}满足:bn= (n∈N*),求{bn}的前n项和公式Tn.
(n∈N*),求{bn}的前n项和公式Tn.
(1)求{an}的通项公式;
(2)若数列{bn}满足:bn=
 (n∈N*),求{bn}的前n项和公式Tn.
(n∈N*),求{bn}的前n项和公式Tn.(1) an=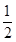 ·(
·(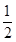 )n-1=(
)n-1=(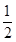 )n,(n∈N*). (2) Tn=(n-1)2n+1+2,n∈N*.
)n,(n∈N*). (2) Tn=(n-1)2n+1+2,n∈N*.
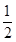 ·(
·(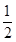 )n-1=(
)n-1=(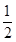 )n,(n∈N*). (2) Tn=(n-1)2n+1+2,n∈N*.
)n,(n∈N*). (2) Tn=(n-1)2n+1+2,n∈N*. 本试题主要是考查了数列的通项公式的求解和数列求和的综合运用。
(1)因为∵Sn=1-an ① ∴Sn+1=1-an+1,②那么可知an+1=-an+1+an,∴an+1=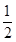 an(n∈N*),由此得到结论。
an(n∈N*),由此得到结论。
(2)∵bn= =n·2n(n∈N*),然后结合错位相减法得到数列的和
=n·2n(n∈N*),然后结合错位相减法得到数列的和
(1)因为∵Sn=1-an ① ∴Sn+1=1-an+1,②那么可知an+1=-an+1+an,∴an+1=
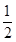 an(n∈N*),由此得到结论。
an(n∈N*),由此得到结论。(2)∵bn=
 =n·2n(n∈N*),然后结合错位相减法得到数列的和
=n·2n(n∈N*),然后结合错位相减法得到数列的和
练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
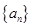 中的相邻两项
中的相邻两项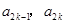 是关于
是关于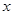 的方程
的方程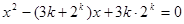 的两个根,且
的两个根,且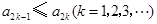 .
.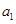 ,
,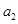 ,
,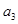 ,
,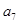 ;
; 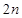 项和
项和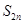 ;
;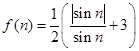 ,
,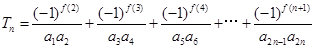 ,
,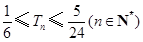 .
.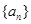 是一个公差为2的等差数列,
是一个公差为2的等差数列,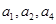 成等比数列.
成等比数列.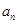 ;
;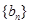 满足
满足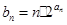 ,设
,设 ,求
,求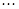
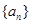 的各项均为正数,
的各项均为正数,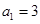 ,前
,前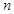 项和为
项和为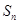 ,
,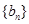 为等比数列,
为等比数列, 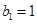 ,
,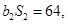
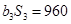 .
.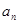 与
与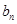 ;
;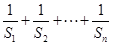 .
. 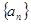 是公差不为0的等差数列,
是公差不为0的等差数列,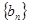 是等比数列,且
是等比数列,且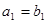 ,
,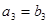 ,
,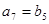 ,
,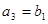
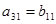
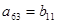
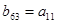
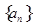 的前
的前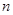 项和为
项和为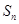 ,且
,且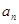 是
是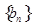 中,
中,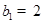 ,点
,点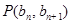 在直线
在直线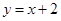 上.
上.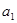 和
和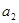 的值;
的值;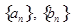 的通项
的通项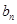 ;
;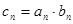 ,求数列
,求数列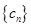 的前n项和
的前n项和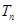 .
.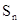 ,若
,若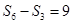 ,则
,则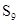 =____________.
=____________.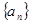 的前n项和,若
的前n项和,若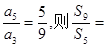 ( )
( )