题目内容
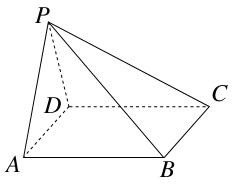
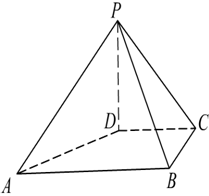
(14分)如图,四棱锥P—ABCD的底面是A B=2,BC=
B=2,BC=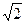 的矩形,侧面PAB
的矩形,侧面PAB
是等边三角形,且侧面PAB⊥底面ABCD
(I)证明:侧面PAB⊥侧面PBC;
(II)求侧棱PC与底面ABCD所成的角;
(III)求直线AB与平面PCD的距离.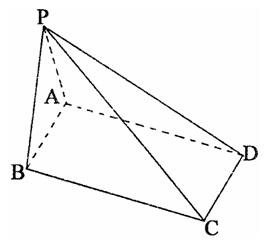
(I)证明:在矩形ABCD中,BC⊥AB
又∵面PAB⊥底面ABCD侧面PAB∩底面ABCD=AB
∴BC ⊥侧面PAB
⊥侧面PAB
又∵BC 侧面PBC
侧面PBC
∴侧面PAB⊥侧面PBC)
(II)解:取AB中点E,连结PE、CE
又∵△PAB是等边三角 形
形
∴PE⊥AB
又∵侧面PAB⊥底面ABCD,∴PE⊥面ABCD
∴∠PCE为侧棱PC与底面ABCD所成角
在Rt△PEC中,∠PCE=45°为所求
(Ⅲ)解:在矩形ABCD中,AB//CD
∵ CD
CD 侧面PCD,AB
侧面PCD,AB 侧面PCD,∴AB//侧面PCD
侧面PCD,∴AB//侧面PCD
取CD中点F,连EF、PF,则EF⊥ AB
AB
又∵PE⊥AB
∴AB⊥平面PEF
又∵AB//CD
∴CD⊥平面PEF
∴平面PCD⊥平面PEF
作EG⊥PF,垂足为G,则EC⊥平面PCD
在Rt△PEF中,EG= 为所求
为所求
解析

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
已知点A(-3,1,4),则点A关于x轴的对称点的坐标为( )
| A.(-3,1,-4) | B.(3,-1,-4) | C.(-3,-1,-4) | D.(-3,,1,-4) |
已知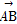 =(1,5,-2),
=(1,5,-2),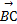 =(3,1,z),若
=(3,1,z),若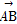 ⊥
⊥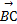 ,
,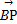 =(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为( )
=(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为( )
A.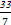 ,- ,-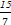 ,4 ,4 | B.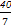 ,- ,-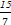 ,4 ,4 |
C.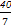 ,-2,4 ,-2,4 | D.4,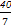 ,-15 ,-15 |
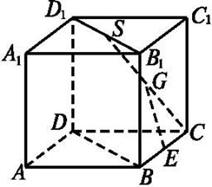
 ,AA1=4,点D是AB的中点
,AA1=4,点D是AB的中点 AC⊥BC1;
AC⊥BC1; 的平面角的正切值.
的平面角的正切值.
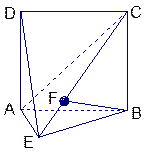

 中,
中, ,
, ,
,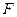 为
为 上的点,且
上的点,且 ,
,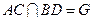 .
.
 平面
平面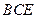 ;
;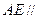 平面
平面 ;
; 的体积.
的体积.