题目内容
(5分)(2011•湖北)若实数a,b满足a≥0,b≥0,且ab=0,则称a与b互补,记φ(a,b)= ﹣a﹣b那么φ(a,b)=0是a与b互补的( )
﹣a﹣b那么φ(a,b)=0是a与b互补的( )
| A.必要不充分条件 | B.充分不必要的条件 |
| C.充要条件 | D.既不充分也不必要条件 |
C
解析试题分析:我们先判断φ(a,b)=0⇒a与b互补是否成立,再判断a与b互补⇒φ(a,b)=0是否成立,再根据充要条件的定义,我们即可得到得到结论.
解:若φ(a,b)= ﹣a﹣b=0
﹣a﹣b=0
则 =(a+b)
=(a+b)
两边平方解得ab=0,故a,b至少有一为0,
不妨令a=0则可得|b|﹣b=0,故b≥0,即a与b互补
而当a与b互补时,
易得ab=0
此时 ﹣a﹣b=0
﹣a﹣b=0
即φ(a,b)=0
故φ(a,b)=0是a与b互补的充要条件
故选C
点评:本题考查的知识点是必要条件、充分条件与充要条件的,其中判断φ(a,b)=0⇒a与b互补与a与b互补⇒φ(a,b)=0的真假,是解答本题的关键.

练习册系列答案
相关题目
在三角形ABC中,“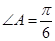 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题中,真命题是( )
A. 是 是 的充分不必要条件 的充分不必要条件 |
B.“已知 ,且 ,且 ,则 ,则 或 或 ”是真命题 ”是真命题 |
C.命题“ ”的否定是“ ”的否定是“ ” ” |
D.“若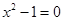 ,则 ,则 或 或 ”的否命题为“ ”的否命题为“ ,则 ,则 或 或 ” ” |
设 、
、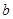 是实数,则“
是实数,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列命题中假命题有 ( )
① ,使
,使 是幂函数;
是幂函数;
② ,使
,使 成立;
成立;
③ ,使
,使 恒过定点;
恒过定点;
④ ,不等式
,不等式 成立的充要条件
成立的充要条件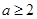 .
.
| A.3个 | B.2个 | C.1个 | D.0个 |
[2014·徐州检测]用分析法证明:欲使①A>B,只需②C<D,这里①是②的( )
| A.充分条件 | B.必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
[2014·孝感统考]已知命题p:?x∈R,使sinx= ;命题q:?x∈R,都有x2+x+1>0.给出下列结论:
;命题q:?x∈R,都有x2+x+1>0.给出下列结论:
①命题p∧q是真命题;②命题( p)∨q是真命题;③命题(
p)∨q是真命题;③命题( p)∨(
p)∨( q)是假命题;④命题p∧(
q)是假命题;④命题p∧( q)是假命题.
q)是假命题.
其中正确的是( )
| A.②③ | B.②④ | C.③④ | D.①②③ |
如果命题“綈(p∧q)”是真命题, 则( )
| A.命题p、q均为假命题 |
| B.命题p、q均为真命题 |
| C.命题p、q中至少有一个是真命题 |
| D.命题p、q中至多有一个是真命题 |
 ;
; ;
; ,
, ,则“
,则“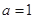 ”是“
”是“ ”的必要不充分条件;
”的必要不充分条件; ,
,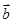 为单位向量,其夹角为
为单位向量,其夹角为 ,若
,若 ,则
,则 .
.