题目内容
13.已知函数f(x)=mx-sinx-cosx,g(x)=(ax-1)cosx-2sinx(a>0).(Ⅰ)若函数y=f(x)在(-∞,+∞)上是单调递减函数,求实数m的最大值;
(Ⅱ)若m=1,且对于任意x∈[0,$\frac{π}{2}$],都有不等式f(x)≥g(x)成立,求实数a的取值范围.
分析 (1)求导,利用导函数和原函数单调性关系转换成最值问题,进行求解即可;
(2)对式子 整理可得:x+sinx≥axcosx,分别讨论,转换成求函数最值:a≤$\frac{1}{cosx}$+$\frac{tanx}{x}$,
构造函数,利用导数判断函数的单调性,进而利用极限的方法求出函数的最小极限值.
解答 解:(1)f(x)=mx-sinx-cosx,
∴f'(x)=m-cosx+sinx
=m+$\sqrt{2}$sin(x-$\frac{π}{4}$)≤0恒成立,
∴m≤-$\sqrt{2}$,
∴实数m的最大值为-$\sqrt{2}$;
(2)m=1,
∴x+sinx≥axcosx,
当x=0,或x=$\frac{π}{2}$时,显然成立,
当x∈(0,$\frac{π}{2}$)时,
a≤$\frac{1}{cosx}$+$\frac{tanx}{x}$,
令h(x)=$\frac{1}{cosx}$+$\frac{tanx}{x}$,
$\frac{1}{cosx}$显然在此区间是增函数,令p(x)=$\frac{tanx}{x}$,
∴p'(x)=$\frac{x-\frac{1}{2}sin2x}{{x}^{2}co{s}^{2}x}$,令r(x)=x-$\frac{1}{2}$sin2x,
∴r'(x)=1-$\frac{1}{2}$cos2x>0,
∴r(x)>r(0)=0,
∴p'(x)>0,
∴h(x)在区间(0,$\frac{π}{2}$)上递增,
∴h(x)>2,
故a的范围为a≤2.
点评 考查了函数求导和恒成立问题的转换,利用导函数判断函数的单调性,利用极限求极限值.

练习册系列答案
相关题目
3.函数y=kx2-4x-8在区间[5,10]上是减少的,在实数k的取值范围是( )
| A. | (-$∞,\frac{1}{5}$)∪[$\frac{2}{5},+∞$] | B. | [0,$\frac{1}{5}$] | C. | (0,$\frac{1}{5}$] | D. | (-$∞,\frac{1}{5}$] |
5.已知f(x)=$\left\{\begin{array}{l}(2a-1)x+4a,x<1\\-x+1,x≥1\end{array}$是定义在R上的减函数,则a的取值范围是( )
| A. | $[\frac{1}{6},\frac{1}{2})$ | B. | $[\frac{1}{3},\frac{1}{2}]$ | C. | $(\frac{1}{6},\frac{1}{2}]$ | D. | $[\frac{1}{3},\frac{1}{2}]$ |
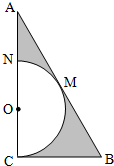 如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.
如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.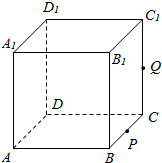 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}.时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}.时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.