题目内容
一条动圆圆心在抛物线上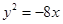 ,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
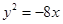 ,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()| A.x=4 | B.y=4 | C.x=2 | D.x=-2 |
C
本题考查抛物线定义的应用。
点拨:掌握抛物线定义是解题关键。抛物线上的点到焦点的距离等于到准线的距离。
解答:根据抛物线上的点到焦点的距离等于到准线的距离,动圆圆心到点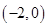 (焦点)的距离等于到准线x=2的距离,而动圆圆心到直线x=2的距离的距离等于半径,故直线x=2即为动圆的公切线。
(焦点)的距离等于到准线x=2的距离,而动圆圆心到直线x=2的距离的距离等于半径,故直线x=2即为动圆的公切线。
点拨:掌握抛物线定义是解题关键。抛物线上的点到焦点的距离等于到准线的距离。
解答:根据抛物线上的点到焦点的距离等于到准线的距离,动圆圆心到点
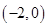 (焦点)的距离等于到准线x=2的距离,而动圆圆心到直线x=2的距离的距离等于半径,故直线x=2即为动圆的公切线。
(焦点)的距离等于到准线x=2的距离,而动圆圆心到直线x=2的距离的距离等于半径,故直线x=2即为动圆的公切线。
练习册系列答案
相关题目
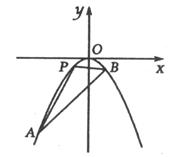
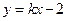 与抛物线C:
与抛物线C: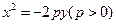 交于A,B两点,
交于A,B两点,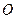 为坐标原点,
为坐标原点,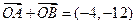 。
。
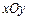 中的抛物线
中的抛物线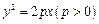 的焦点
的焦点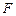 作一条倾斜角为
作一条倾斜角为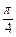 的直线与抛物线相交于A、B两点.
的直线与抛物线相交于A、B两点.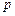 表示A、B之间的距离;
表示A、B之间的距离;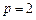 时,求
时,求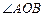 的余弦值.
的余弦值.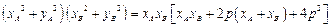 .
.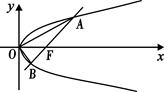
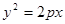 的焦点与椭圆
的焦点与椭圆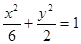 的右焦点重合,则
的右焦点重合,则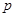 的值为 ( )
的值为 ( )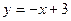 与
与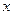 轴、
轴、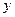 轴分别交于
轴分别交于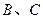 ,抛物线
,抛物线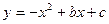 经过点
经过点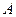 是抛物线与
是抛物线与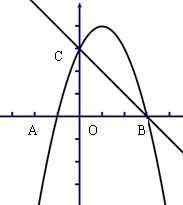
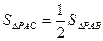 ,求P点坐标。
,求P点坐标。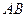 ⊥
⊥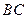 ,
,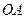 ∥
∥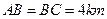 ,
,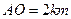 ,
, 曲线段
曲线段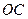 是以点
是以点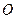 为顶
为顶 点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落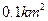 ).
).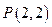 为
为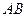 的中点,则抛物线C的方程为
的中点,则抛物线C的方程为 
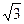 ,则M到该抛物线焦点的距离为
,则M到该抛物线焦点的距离为